A terribly large number of hostages, say $n=1000$ people, are standing in a circle. The terrorists claim that once the circle is formed, they’ll ask the poor people to kill the $k=4$-th people to the left of him/her. Since the queue is circular, when it comes to the people standing on the leftmost spots, the next person to be killed may be from the first several ones as the procedure can repeat untill there’s only one person alive. This problem is named after Flavius Josephus, a Jewish historian living in the 1st century. According to Josephus’ account of the siege of Yodfat, he and his 40 soldiers were trapped in a cave by Roman invaders and faced with the aforementioned dilemma except that his problem was easier with $(n,k)=(41,1)$.

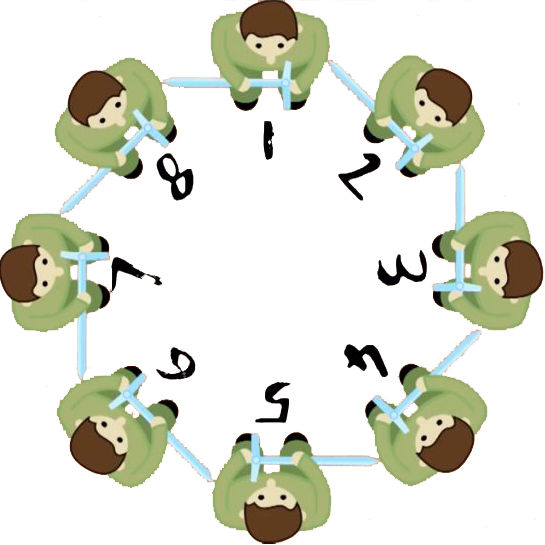
We call it a dilemma because there is one opportunity where Josephus can live, and finding the only spot that stands till the end is not easy. In the illustration above shows a simple example when there’re $n=8$ people in the circle. Let’s say $k=1$, namely a hostage always kills the person standing right to the left of him/her. Person 1 first kills person 2, and then person 3 kills 4 and so on. The procedure is as follows (numbers in red mean dead people):

• 1, 2, 3, 4, 5, 6, 7, 8 (before start)
• 1, 2, 3, 4, 5, 6, 7, 8 (1st round)
• 1, 2, 3, 4, 5, 6, 7, 8 (2nd round)
• 1, 2, 3, 4, 5, 6, 7, 8 (3rd round, end of killing)

So in the case $(n,k)=(8,1)$, Josephus should stand on the 1st spot. Let’s denote this as $f(8,1)=1$ just to make it look more mathematical. The general Josephus problem, therefore, becomes finding $\forall n,k\in\mathbb{N}_+$ the optimal index¹ $f(n,k)$.

Special Case: $k=1$

There exists a closed-form solution when $k=1$, and I’d like to share with you here the intuition behind it. Consider the cases where $n$ is some power of $2$, e.g. $n=2,4,8,16,\ldots$ Like the example above, you’ll notice that a problem of some higher power of $2$, say $n=8\equiv 2^3$, reduces to the sub-power one that is $n=4\equiv 2^2$ and so forth. It can be easily proved by mathematical induction that whenever $n=2^m$ for some $m\ge 1$, the last one standing is always person 1.

With the result above we may tackle problems that are slightly more general, i.e. $2^m < n < 2^{m+1}$ for some $m\ge 1$. Notice by reverse thinking the problem will always reduce to the case $n=2^m$ as we’re killing people one by one, and at that moment we know the first person who kills is the person who lives till the end. There’re in total $n-2^m$ people died before our winner wields his sword against his ally. Since

$$ n < 2^{m+1} \Rightarrow 2n - 2^{m+1} < n \Rightarrow n - 2^m < \left\lfloor\frac{n}{2}\right\rfloor, $$

we know the 1st round is not yet finished and thus the winner is

$$ f(n,k) = 2(n-2^m)+1 = 2(n-2^{\lfloor\log_2 n\rfloor})+1. $$

As a conclusion, if Josephus is smart enough to come up with this solution, he should choose the $2\times(41-32)+1=19$-th place.

General Case

There is unfortunately no general solution for any $n$ and $k$. However, with the help of a computer we may come up with an algorithm that simulates the process in $O(n)$ time, regardless of $k$. The Python codes are as follows:

def Josephus(n, k):
    player = list(range(1, n + 1))
    idx_prev = 0
    while True:
        if len(player) == 1: return player[0]
        idx = (k + idx_prev) % len(player)
        player.pop(idx)
        idx_prev = idx


Josephus(1000, 4)

This prints 763, which is the answer to the first question above.