Bitcoin Inter-exchange Price Spread Prediction
2017-05-21
Price prediction is thought to be very difficult for any equity, however the price spread between two exchanges may not. We look into the price spread between two of the largest Bitcoin exchanges: Bitstamp and BTC-E.
Step 1: Import All Packages
import quandl
import cmocean
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from pytrends.request import TrendReq
from scipy import stats as ss
from datetime import datetime as dt
from arch.unitroot import PhillipsPerron, ADF
from matplotlib import pyplot as plt
from matplotlib import dates as mdates
from statsmodels.graphics.api import qqplot
pytrend = TrendReq('[email protected]', 'aaaaaaaaaa', hl='en-US', tz=360, custom_useragent=None)
warnings.filterwarnings('ignore')
quandl.ApiConfig.api_key = 'aaaaaaaaaaaaaaa'
pd.set_option("display.width",999)
plt.rcdefaults()
plt.style.use('seaborn-paper')
plt.rcParams['axes.facecolor']='w'
plt.rcParams['axes.grid']=False
plt.rcParams['font.family'] = 'serif'
plt.rcParams['figure.figsize'] = [12, 4]
Step 2: Data Retrieving and Cleaning
Data source: https://www.quandl.com/data/.
exchangelist = [
'BTCE',
'KRAKEN',
'BITFINEX',
'BITSTAMP',
# 'COINBASE',
'ROCK',
'HITBTC',
'ITBIT',
'BITBAY',
'BITKONAN',
'CBX',
'VCX'
]
n = len(exchangelist)
print('there are {} exchanges in total'.format(n))
there are 11 exchanges in total
exchanges = [quandl.get('BCHARTS/' + e + 'USD') for e in exchangelist]
for i in range(n):
daterange = exchanges[i].index.tolist()
print('{:>8}'.format(exchangelist[i]), daterange[0].date(), daterange[-1].date())
BTCE 2011-08-14 2017-05-19
KRAKEN 2014-01-07 2017-05-19
BITFINEX 2013-03-31 2016-12-22
BITSTAMP 2011-09-13 2017-05-19
ROCK 2011-11-12 2017-05-19
HITBTC 2013-12-27 2017-05-19
ITBIT 2013-08-25 2017-05-19
BITBAY 2014-05-16 2017-05-19
BITKONAN 2013-07-02 2017-05-19
CBX 2011-07-05 2017-04-16
VCX 2011-12-25 2017-05-19
start_date = pd.to_datetime('2014-07-01')
mid_date = pd.to_datetime('2016-01-01')
end_date = pd.to_datetime('2016-07-01')
price = pd.concat([e.ix[start_date:end_date,'Close'] for e in exchanges], join='outer', axis=1)
volume = pd.concat([e.ix[start_date:end_date,'Volume (Currency)'] for e in exchanges], join='outer', axis=1)
price.columns = exchangelist
volume.columns = exchangelist
price = price[price > 0].fillna(method='ffill').fillna(method='bfill')
volume = price[volume > 0].fillna(method='ffill').fillna(method='bfill')
print(price.describe())
BTCE KRAKEN BITFINEX BITSTAMP ROCK HITBTC ITBIT BITBAY BITKONAN CBX VCX
count 732.000000 732.000000 732.000000 732.000000 732.000000 732.000000 732.000000 732.000000 732.000000 732.000000 732.000000
mean 359.045682 363.799398 363.647027 363.204795 363.963907 373.581913 362.888860 367.052036 369.847240 367.836366 388.325161
std 119.611681 122.473245 122.182031 122.020091 121.643524 115.354405 121.729241 125.084653 123.984738 119.057448 94.745641
min 170.000000 175.000000 182.000000 171.410000 185.000000 186.760000 183.160000 186.890000 171.030000 200.040000 210.000001
25% 245.123250 249.669390 249.235000 249.047500 249.887500 272.900000 249.252500 253.750000 254.972500 254.757500 312.249915
50% 349.933000 358.429990 353.825000 356.495000 355.015000 357.610000 353.475000 359.995000 360.765000 365.005000 380.000000
75% 429.812500 430.136262 433.410000 432.535000 433.282500 438.695000 432.302500 435.082500 442.192500 432.992500 425.000000
max 729.855000 765.490000 769.500000 766.620000 767.800000 768.590000 767.180000 999.000000 771.670000 690.000000 658.000000
Step 3: Data Analysis
%config InlineBackend.figure_format = 'retina'
min_exchange = pd.Series([np.argmin(price.iloc[i], axis=0) for i in range(len(price))],
index=price.index).apply(lambda fn: exchangelist.index(fn))
max_exchange = pd.Series([np.argmax(price.iloc[i], axis=0) for i in range(len(price))],
index=price.index).apply(lambda fn: exchangelist.index(fn))
dmin = price.min(axis=1)
dmax = price.max(axis=1)
thermal = cmocean.cm.thermal
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(n):
ax.plot((price.index[0], price.index[0]), (0, 0), c=thermal(i/n), label=exchangelist[i])
for i in range(len(price)):
ax.plot((price.index[i], price.index[i]), (0, -dmin[i]), lw=1.5, c=thermal(min_exchange[i]/n))
ax.plot((price.index[i], price.index[i]), (0, dmax[i]), lw=1.5, c=thermal(max_exchange[i]/n))
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
ax.set_ylim(-1500,1500)
plt.legend(loc='lower center', frameon=0, ncol=n//2)
plt.tight_layout()
plt.savefig('price1.pdf')
plt.show()
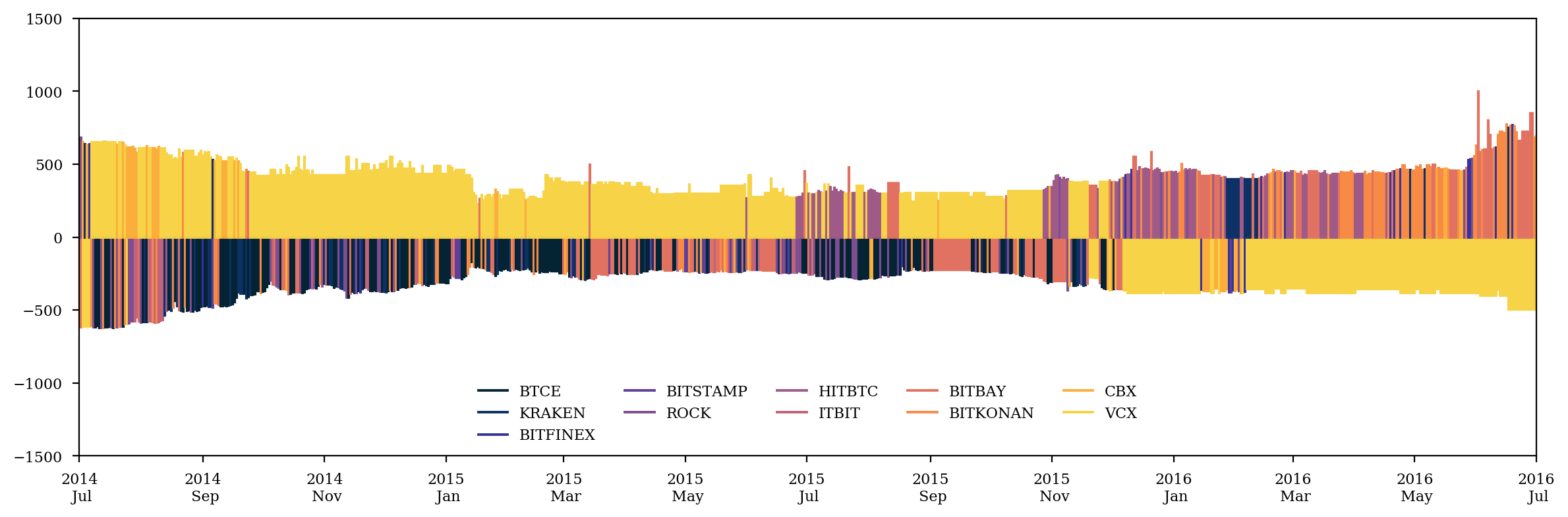
active_price = price * (price.diff() != 0)
active_price = active_price[active_price > 0]
err_count = np.isnan(active_price).sum()
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax1 = fig.add_subplot(111)
(100*max_exchange.value_counts().sort_index().reindex(range(len(exchangelist))).fillna(0)/len(price)).plot.bar(ax=ax1, color='c', align='center', alpha=.5, label='% being highest')
(100*min_exchange.value_counts().sort_index().reindex(range(len(exchangelist))).fillna(0)/len(price)).plot.bar(ax=ax1, color='r', align='center', alpha=.5, label='% being lowest')
ax1.set_ylim(-5,80)
ax1.set_ylabel('%')
plt.xticks(range(len(err_count)), err_count.index.tolist(), rotation=0)
ax1.legend(loc='upper left', frameon=0)
ax2 = ax1.twinx()
err_count.plot(ax=ax2, marker='o', color='r', alpha=.5, label='total number of error days')
ax2.set_xlim(-.5,len(err_count)-.5)
ax2.set_xticks(range(len(err_count)), err_count.index.tolist())
ax2.legend(loc='upper right', frameon=0)
ax2.set_ylim(-35,500)
# plt.grid(None)
plt.tight_layout()
plt.show()
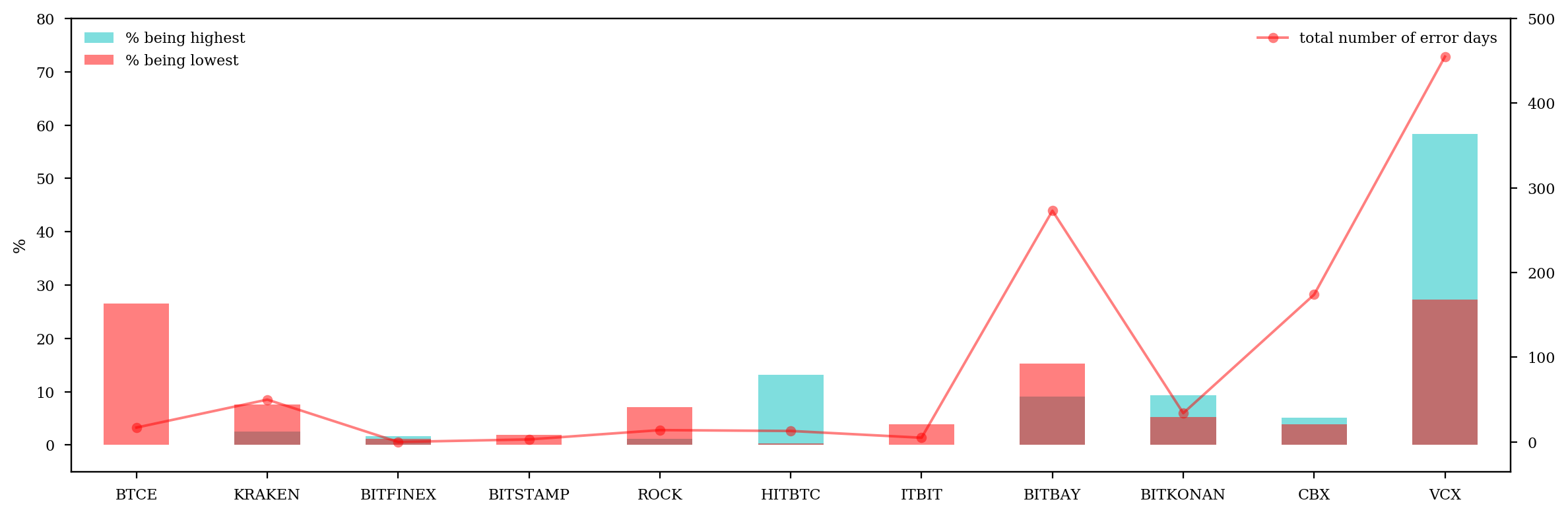
irr_exchanges = [10,9,8,7,5,0] # delete those that have over 200 error days, or dominate over 10% of all time range
n -= len(irr_exchanges)
active_price.drop(active_price.columns[[irr_exchanges]], axis=1, inplace=1)
for i in irr_exchanges:
exchangelist.pop(i)
%config InlineBackend.figure_format = 'retina'
min_exchange = pd.Series([np.argmin(active_price.iloc[i], axis=0) for i in range(len(active_price))], index=active_price.index).apply(lambda fn: exchangelist.index(fn))
dmin = active_price.min(axis=1)
max_exchange = pd.Series([np.argmax(active_price.iloc[i], axis=0) for i in range(len(active_price))], index=active_price.index).apply(lambda fn: exchangelist.index(fn))
dmax = active_price.max(axis=1)
thermal = cmocean.cm.thermal
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(n):
ax.plot((active_price.index[0], active_price.index[0]), (0, 0), c=thermal(i/n), label=exchangelist[i])
for i in range(len(active_price)):
ax.plot((active_price.index[i], active_price.index[i]), (0, -dmin[i]), lw=1.5, c=thermal(min_exchange[i]/n))
ax.plot((active_price.index[i], active_price.index[i]), (0, dmax[i]), lw=1.5, c=thermal(max_exchange[i]/n))
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
ax.set_ylim(-1500,1500)
plt.legend(loc='lower center', frameon=0, ncol=n)
plt.tight_layout()
plt.savefig('price2.pdf')
plt.show()
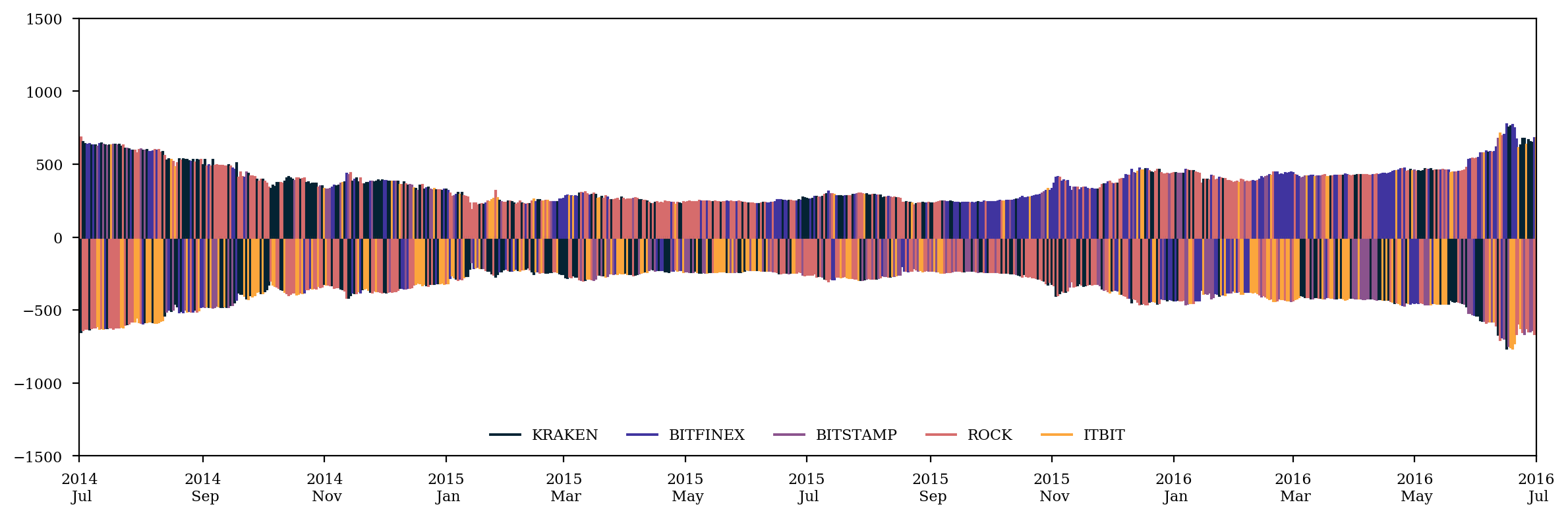
%config InlineBackend.figure_format = 'retina'
err_count = np.isnan(active_price).sum()
plt.close()
fig = plt.figure()
ax1 = fig.add_subplot(111)
(100*max_exchange.value_counts().sort_index().reindex(range(len(exchangelist))).fillna(0)/len(price)).plot.bar(ax=ax1, color='c', align='center', alpha=.5, label='% being highest')
(100*min_exchange.value_counts().sort_index().reindex(range(len(exchangelist))).fillna(0)/len(price)).plot.bar(ax=ax1, color='r', align='center', alpha=.5, label='% being lowest')
ax1.set_ylim(-5,80)
ax1.set_ylabel('%')
plt.xticks(range(len(err_count)), err_count.index.tolist(), rotation=0)
ax1.legend(loc='upper left', frameon=0)
ax2 = ax1.twinx()
err_count.plot(ax=ax2, marker='o', color='r', alpha=.5, label='total number of error days')
ax2.set_xlim(-.5,len(err_count)-.5)
ax2.set_xticks(range(len(err_count)), err_count.index.tolist())
ax2.legend(loc='upper right', frameon=0)
ax2.set_ylim(-7,100)
# plt.grid(None)
plt.tight_layout()
plt.show()
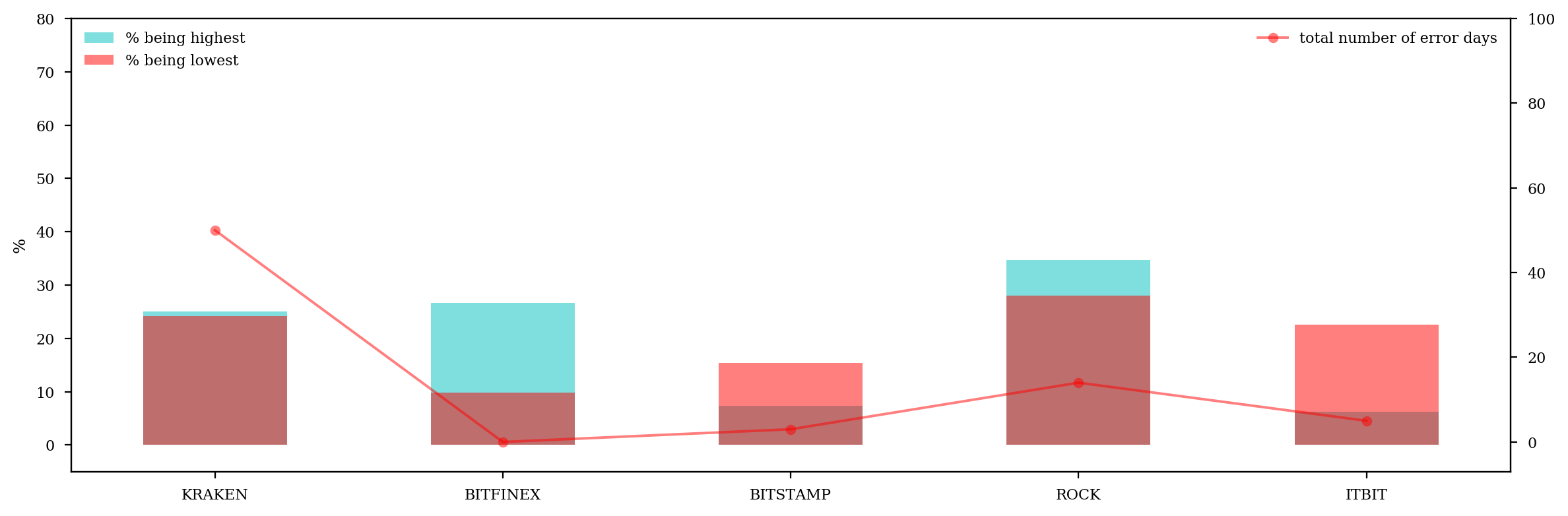
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(n):
ax.plot(active_price.ix[:,i], c=thermal(i/n), label=exchangelist[i])
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.set_xlim(start_date, end_date)
ax.set_ylim(0,1000)
plt.legend(loc='lower center', frameon=0, ncol=n)
plt.tight_layout()
# plt.title('Historical Prices')
plt.savefig('price3.pdf')
plt.show()
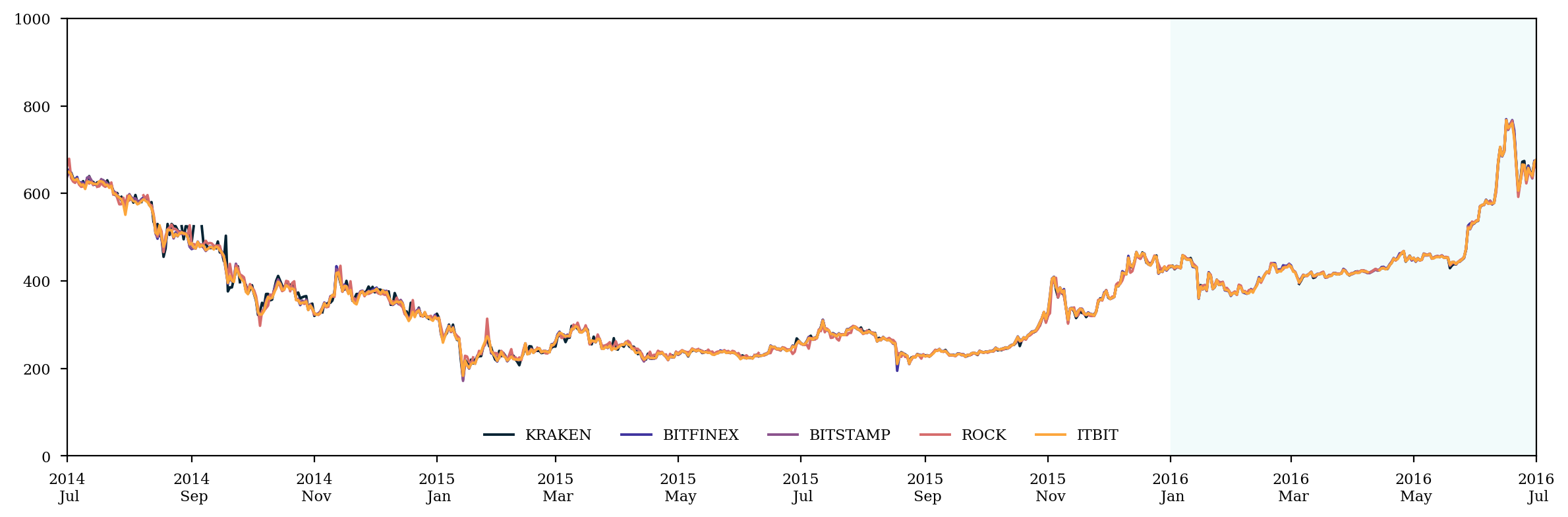
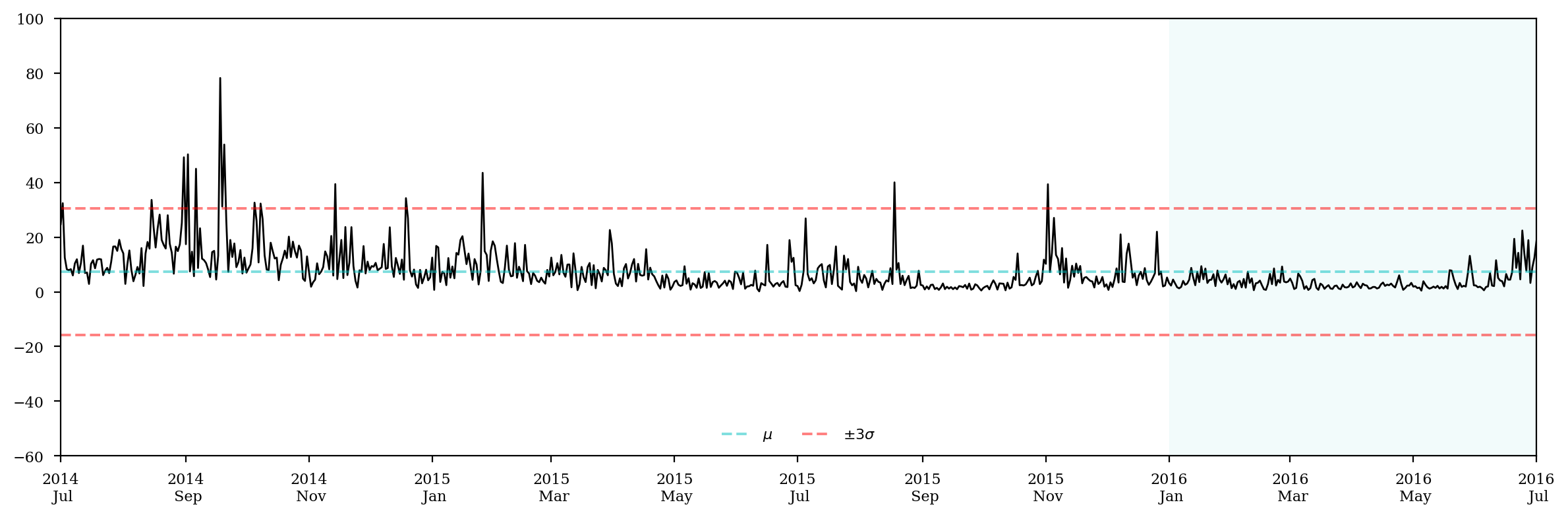
price_spread = active_price.max(axis=1) - active_price.min(axis=1)
price_spread.describe()
count 732.000000
mean 7.418801
std 7.705870
min 0.150000
25% 2.430000
50% 4.914920
75% 9.461703
max 78.191470
dtype: float64
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(price_spread, lw=1,c='k')
ax.axhline(price_spread.mean(), alpha=0.5, ls='--', c='c', label='$\mu$')
ax.axhline(price_spread.mean()+price_spread.std()*3, alpha=0.5, ls='--', c='r', label='$\pm3\sigma$')
ax.axhline(price_spread.mean()-price_spread.std()*3, alpha=0.5, ls='--', c='r')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.set_xlim(start_date, end_date)
ax.set_ylim(-60,100)
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=2)
# plt.title('Price Spreads')
plt.savefig('spread.pdf')
plt.show()
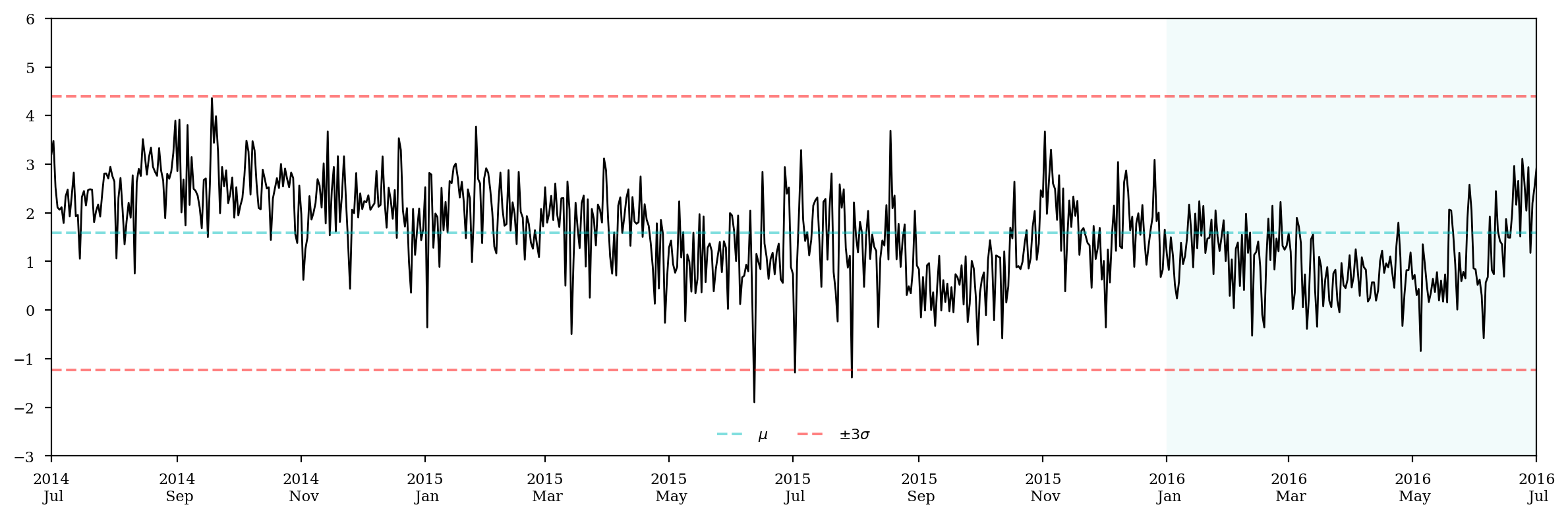
log_price_spread = np.log(price_spread)
log_price_spread.describe()
count 732.000000
mean 1.584788
std 0.939405
min -1.897120
25% 0.887891
50% 1.592275
75% 2.247244
max 4.359161
dtype: float64
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(log_price_spread, c='k',lw=1,label='')
ax.axhline(log_price_spread.mean(), alpha=0.5, ls='--', c='c', label='$\mu$')
ax.axhline(log_price_spread.mean()+log_price_spread.std()*3, alpha=0.5, ls='--', c='r',label='$\pm3\sigma$')
ax.axhline(log_price_spread.mean()-log_price_spread.std()*3, alpha=0.5, ls='--', c='r')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.set_ylim(-3,6)
ax.set_xlim(start_date, end_date)
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=2)
# plt.title('Log Price Spreads')
plt.savefig('logspread.pdf')
plt.show()
print(ADF(log_price_spread, trend='c'), '\n')
print(PhillipsPerron(log_price_spread, trend='c'), '\n')
Augmented Dickey-Fuller Results
=====================================
Test Statistic -2.346
P-value 0.158
Lags 17
-------------------------------------
Trend: Constant
Critical Values: -3.44 (1%), -2.87 (5%), -2.57 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
Phillips-Perron Test (Z-tau)
=====================================
Test Statistic -21.389
P-value 0.000
Lags 20
-------------------------------------
Trend: Constant Critical Values: -3.44 (1%), -2.87 (5%), -2.57 (10%) Null Hypothesis: The process contains a unit root. Alternative Hypothesis: The process is weakly stationary.
def z_norm(s):
return (s - s.mean(axis=0)) / s.std(axis=0)
log_price_spread = z_norm(log_price_spread.rolling(5).mean().fillna(method='bfill'))
log_price_spread.describe()
count 7.320000e+02
mean -4.284976e-15
std 1.000000e+00
min -1.902323e+00
25% -8.414662e-01
50% -1.734537e-02
75% 7.996859e-01
max 2.645812e+00
Name: None, dtype: float64
print(ADF(log_price_spread, trend='nc'), '\n')
print(PhillipsPerron(log_price_spread, trend='nc'), '\n')
Augmented Dickey-Fuller Results
=====================================
Test Statistic -2.229
P-value 0.025
Lags 20
-------------------------------------
Trend: No Trend
Critical Values: -2.57 (1%), -1.94 (5%), -1.62 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
Phillips-Perron Test (Z-tau)
=====================================
Test Statistic -3.321
P-value 0.001
Lags 20
-------------------------------------
Trend: No Trend
Critical Values: -2.57 (1%), -1.94 (5%), -1.62 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(log_price_spread, c='k',lw=1,label='')
ax.axhline(log_price_spread.mean(), alpha=0.5, ls='--', c='c', label='$\mu$')
ax.axhline(log_price_spread.mean()+log_price_spread.std()*3, alpha=0.5, ls='--', c='r',label='$\pm3\sigma$')
ax.axhline(log_price_spread.mean()-log_price_spread.std()*3, alpha=0.5, ls='--', c='r')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.set_ylim(-5,5)
ax.set_yticks(range(-5,6))
ax.set_xlim(start_date, end_date)
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=2)
# plt.title('Log Price Spreads')
plt.savefig('logspreadnorm.pdf')
plt.show()
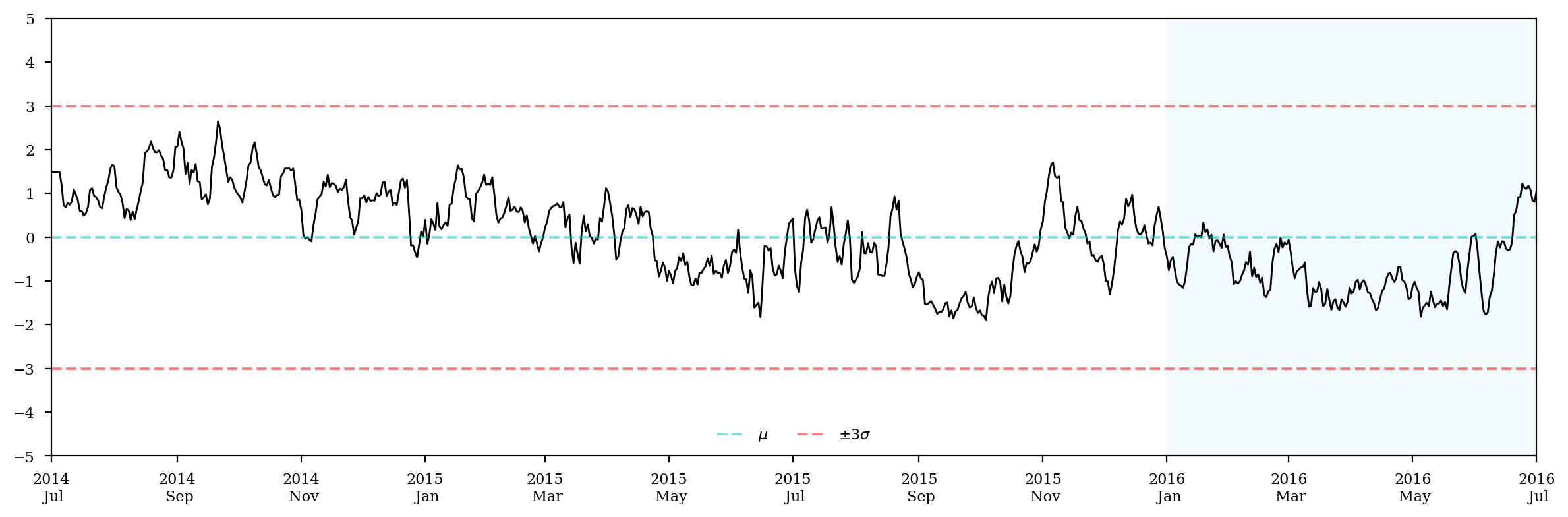
Step 4: Univariate Model - ARMA(p,q)
train = log_price_spread.loc[:mid_date]
test = log_price_spread.loc[mid_date:]
train.name = 'LogPs'
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure(figsize=(8,4))
ax1 = fig.add_subplot(211)
sm.graphics.tsa.plot_acf(train, lags=40, ax=ax1, label='ACF')
ax1.set_ylim(-.55,1.25)
ax1.set_yticks(np.arange(-.5,1.5,.5))
ax1.set_xticks(range(0,40,5))
ax1.set_title('')
handles, labels= ax1.get_legend_handles_labels()
handles = handles[:-len(handles)//3][1::2]
labels = labels[:-len(handles)//3][1::2]
ax1.legend(handles=handles, labels=labels,loc='best', frameon=0, numpoints=2)
ax2 = fig.add_subplot(212)
sm.graphics.tsa.plot_pacf(train, lags=40, ax=ax2, label='PACF')
ax2.set_ylim(-.55,1.25)
ax2.set_yticks(np.arange(-.5,1.5,.5))
ax2.set_xticks(range(0,40,5))
ax2.set_title('')
handles, labels= ax2.get_legend_handles_labels()
handles = handles[:-len(handles)//3][1::2]
labels = labels[:-len(handles)//3][1::2]
ax2.legend(handles=handles, labels=labels,loc='best', frameon=0, numpoints=2)
plt.tight_layout()
plt.savefig('uniacfpacf.pdf')
plt.show()
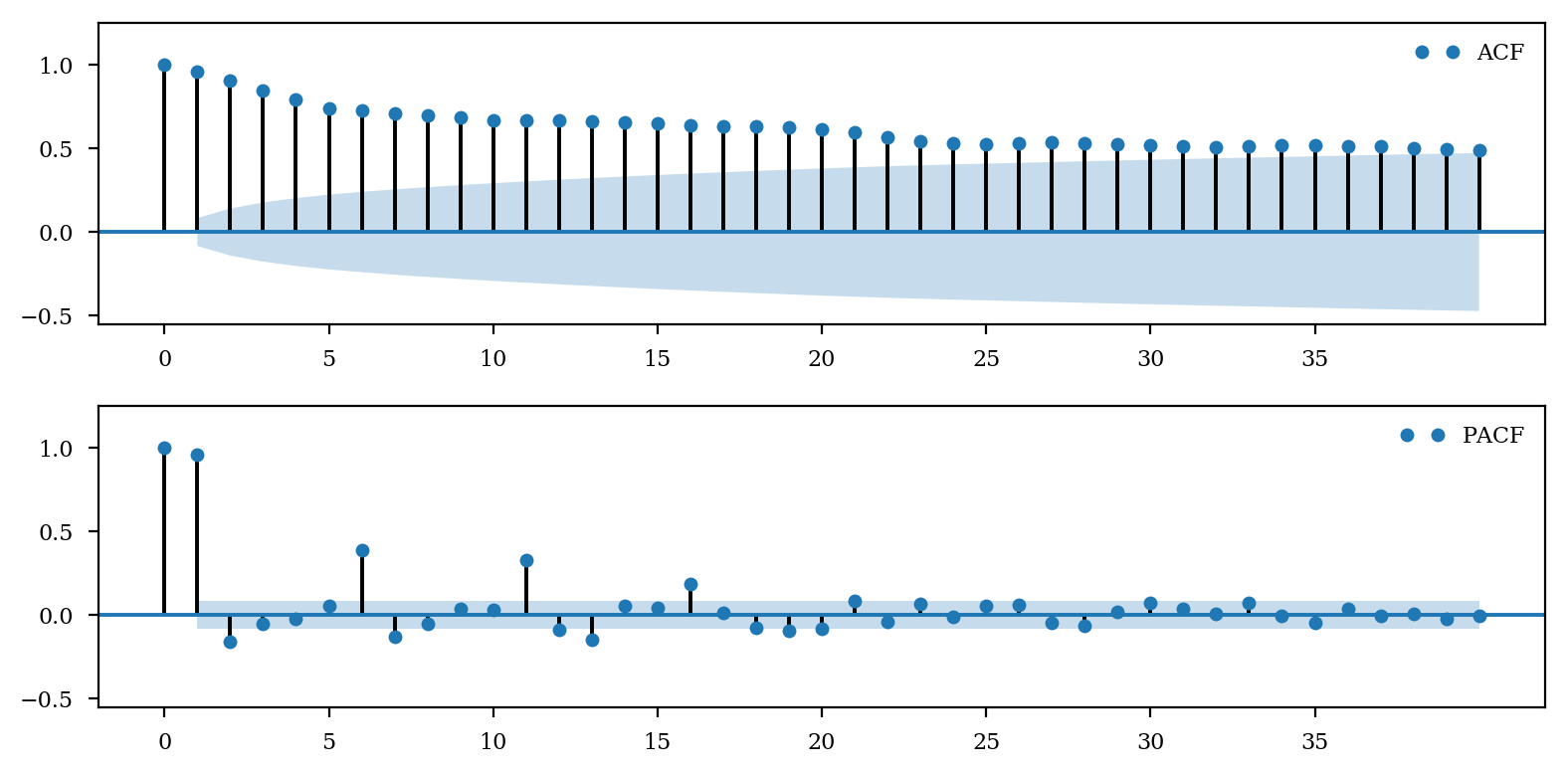
min_aic = min_bic = 1e5
min_aic_order = min_bic_order = (0,0)
for p in range(1,10):
for q in range(6):
model = sm.tsa.ARMA(train, (p, q))
try:
result = model.fit(trend='nc')
stat = abs(sm.stats.durbin_watson(result.resid)-2)
stat_score = (stat <= .01) * 3 + (.01 < stat <= .05) * 2 + (.05 < stat <= .10) * 1
if np.abs(np.concatenate([result.arroots, result.maroots])).min() > 1.05:
aic = result.aic
bic = result.bic
if aic < min_aic:
min_aic = aic
min_aic_order = (p,q)
if bic < min_bic:
min_bic = bic
min_bic_order = (p,q)
print('({},{}) AIC = {:>7.2f}, BIC = {:>7.2f}, |DW-2| = {:.8f} {}'.format(p,q,aic,bic,stat,stat_score*'*'))
except:
continue
print()
print('Minimum AIC = {:.2f} at {}, minimum BIC = {:.2f} at {}'.format(min_aic, min_aic_order, min_bic, min_bic_order))
(1,1) AIC = 113.26, BIC = 126.19, |DW-2| = 0.07497044 *
(1,2) AIC = 113.04, BIC = 130.28, |DW-2| = 0.06298702 *
(2,0) AIC = 111.43, BIC = 124.36, |DW-2| = 0.03723533 **
(2,1) AIC = 112.01, BIC = 129.25, |DW-2| = 0.04461551 **
(2,2) AIC = 113.29, BIC = 134.84, |DW-2| = 0.06107177 *
(3,0) AIC = 111.72, BIC = 128.96, |DW-2| = 0.05226283 *
(3,1) AIC = 113.64, BIC = 135.19, |DW-2| = 0.05401722 *
(4,0) AIC = 113.37, BIC = 134.92, |DW-2| = 0.05788130 *
(4,1) AIC = 115.31, BIC = 141.17, |DW-2| = 0.05672657 *
(5,0) AIC = 113.33, BIC = 139.19, |DW-2| = 0.00835075 ***
Minimum AIC = 111.43 at (2, 0), minimum BIC = 124.36 at (2, 0)
model = sm.tsa.ARMA(train, (2,0))
result = model.fit(trend='nc')
print(result.summary())
ARMA Model Results
==============================================================================
Dep. Variable: LogPs No. Observations: 550
Model: ARMA(2, 0) Log Likelihood -52.713
Method: css-mle S.D. of innovations 0.266
Date: Sun, 21 May 2017 AIC 111.426
Time: 01:10:53 BIC 124.355
Sample: 07-01-2014 HQIC 116.478
- 01-01-2016
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
ar.L1.LogPs 1.1236 0.042 26.763 0.000 1.041 1.206
ar.L2.LogPs -0.1672 0.042 -3.976 0.000 -0.250 -0.085
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.0559 +0.0000j 1.0559 0.0000
AR.2 5.6627 +0.0000j 5.6627 0.0000
-----------------------------------------------------------------------------
Normality test.
sm.stats.jarque_bera(result.resid)[1]
2.6180738344018359e-23
sm.stats.acorr_ljungbox(result.resid, lags=1)[1][0]
0.81633813674691746
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(result.resid, line='45', ax=ax, fit=True)
lines = fig.findobj(lambda x: hasattr(x, 'get_color') and x.get_color() == 'r')
dots = fig.findobj(lambda x: hasattr(x, 'get_color') and x.get_color() == 'b')
[l.set_linewidth(2) for l in lines]
[d.set_alpha(0.3) for d in dots]
# [d.set_color('c') for d in dots]
[d.set_markersize(5) for d in dots]
ax.set_ylim(-3,3)
ax.set_yticks(range(-3,4))
ax.set_xlim(-3,3)
ax.set_xticks(range(-3,4))
plt.tight_layout()
# plt.title('p-value = {}'.format(ss.normaltest(result.resid)[1]))
plt.savefig('uniqqplot.pdf')
plt.show()
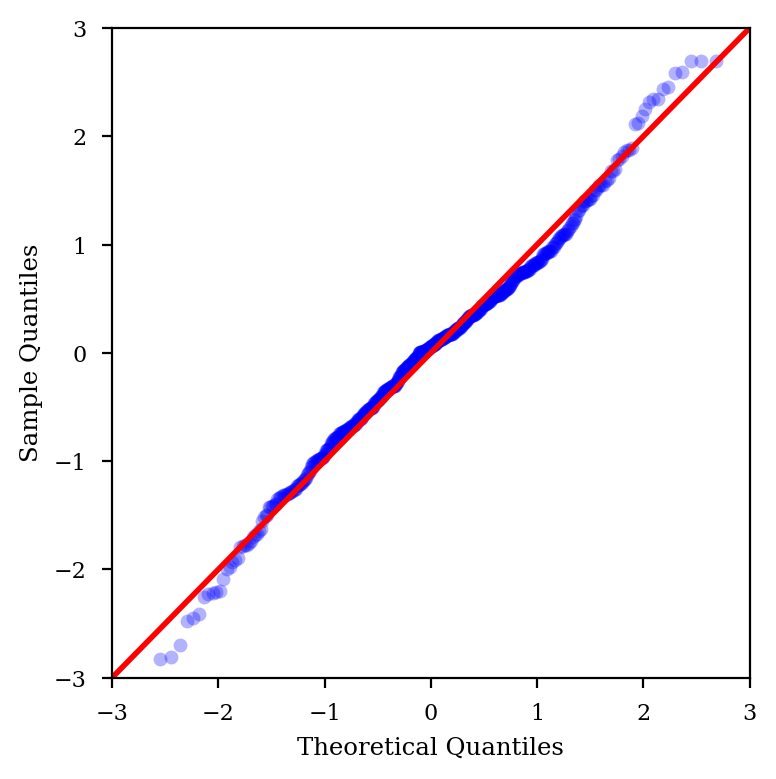
phi = result.arparams * (result.pvalues[:result.k_ar]<=0.05).values
def yhat(y): # y is now nparray of shape (k_ar,2)
ylag = y[::-1]
return ylag.T @ phi
fit = result.fittedvalues
pred = test * np.nan
for i in range(len(phi)):
pred[i] = yhat(train[-1-i-len(phi):-1-i])
for i in range(len(phi), len(test)):
pred[i] = yhat(test[i-len(phi):i])
fcst = result.forecast(len(test))
forecast = pd.Series(fcst[0], index=test.index)
conf_interval = pd.DataFrame(fcst[2], index=test.index)
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(log_price_spread, c='k',lw=1, label='true data')
ax.plot(fit, 'ro-', markevery=10, alpha=0.5, label='insample fitted data')
# ax.plot(result.fittedvalues, 'b-')
ax.plot(pred, 'co-', markevery=10, alpha=0.5, label='outsample point forecast')
ax.plot(forecast, 'c--', label='outsample forecast')
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.fill_between(conf_interval.index, conf_interval.ix[:,0], conf_interval.ix[:,1], color='k', alpha=.1, label='95% conf. interval')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
ax.set_ylim(-5,5)
ax.set_yticks(range(-5,6))
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=5)
# plt.title('First Difference Log Price Spreads')
plt.savefig('unifit1.pdf')
plt.show()
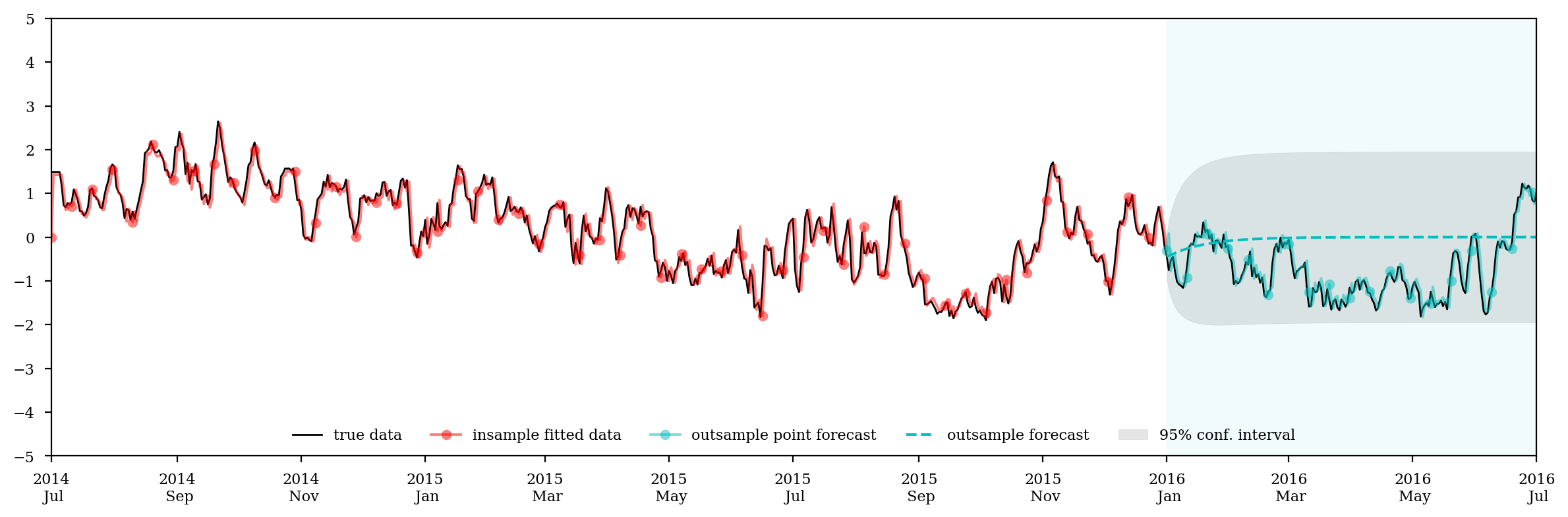
temp_date = pd.to_datetime('2015-12-01')
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(log_price_spread, c='k',lw=1, label='true data')
ax.plot(fit, 'ro-', markevery=5, alpha=0.5, label='insample fitted data')
ax.plot(pred, 'co-', markevery=5, alpha=0.5, label='outsample point forecast')
ax.plot(forecast, 'c--', alpha=0.5, label='outsample forecast')
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.fill_between(conf_interval.index, conf_interval.ix[:,0], conf_interval.ix[:,1], color='k', alpha=.1, label='95% conf. interval')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=1))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(temp_date, end_date)
ax.set_ylim(-5,5)
ax.set_yticks(range(-5,6))
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=5)
# plt.title('First Difference Log Price Spreads')
plt.savefig('unifit2.pdf')
plt.show()
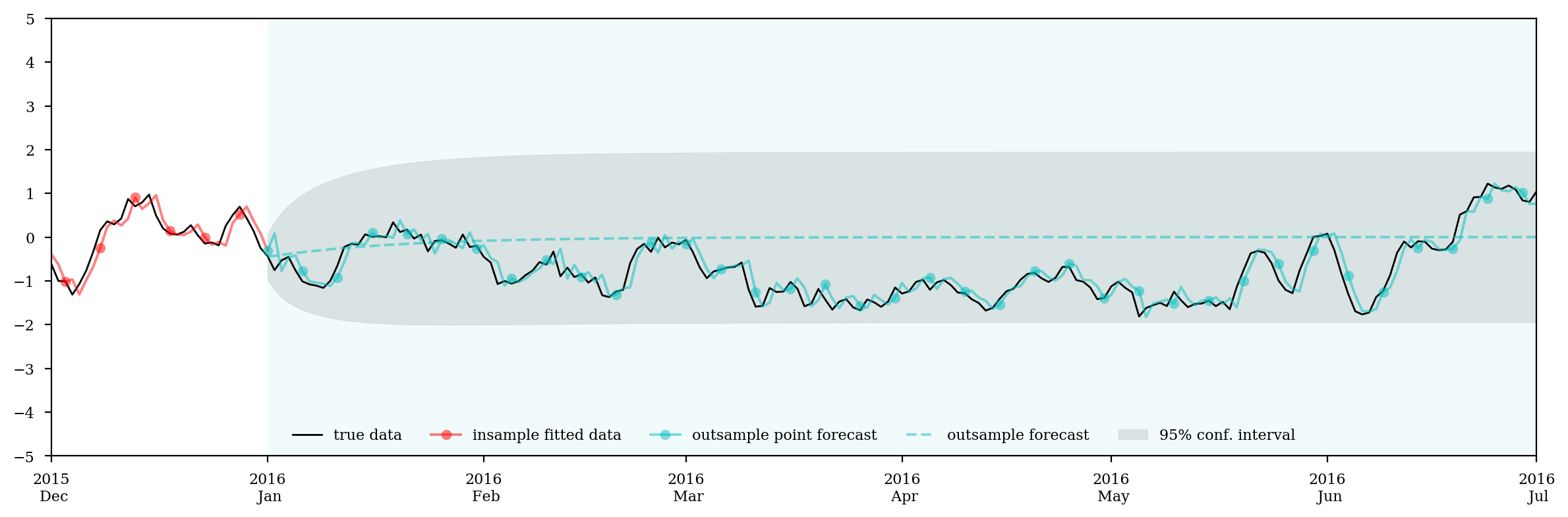
MASE (Mean Absolute Scaled Error): https://en.wikipedia.org/wiki/Mean_absolute_scaled_error
- Better than MAPE: MASE is symmetric while MAPE punishes on negative errors
- Better than RMSE: scaled to the data
- Better than R-squares: parameter number irrelavant
- Better than AUC and Predictive Likelihood: easier to compute
def mase(data, pred):
error = data - pred
ydiff = data.diff().dropna()
return error.abs().mean() / ydiff.abs().mean()
mase_uni_is = mase(train, fit)
mase_uni_osp = mase(test, pred)
mase_uni_os = mase(test, forecast)
print('MASE insample is {:.3f}'.format(mase_uni_is))
print('MASE outsample point is {:.3f}'.format(mase_uni_osp))
print('MASE outsample is {:.3f}'.format(mase_uni_os))
MASE insample is 0.996
MASE outsample point is 0.991
MASE outsample is 4.704
Step 5: Multivariate Model - ARIMAX(p,d,q)
data = [
'BCHAIN/ATRCT', # Bitcoin Median Transaction Confirmation Time
'BCHAIN/CPTRA', # Bitcoin Cost Per Transaction
'BCHAIN/DIFF', # Bitcoin Mining Difficulty
'BCHAIN/TVTVR', # Bitcoin Trade Volume vs Transaction Volume Ratio
]
ind = [quandl.get(d)[start_date:end_date] for d in data]
max_volume = ((volume.apply(lambda v:v.index, axis=1).T == max_exchange.apply(lambda i:exchangelist[i])).T * volume).sum(axis=1)
min_volume = ((volume.apply(lambda v:v.index, axis=1).T == min_exchange.apply(lambda i:exchangelist[i])).T * volume).sum(axis=1)
trade_volume = max_volume + min_volume
transaction_volume = (trade_volume * ind[-1].T).T
ind[-1] = transfer_volume = transaction_volume.Value - trade_volume
dataset = pd.concat([price_spread, trade_volume] + ind, axis=1, join='outer')
dataset.columns = ['Ps', 'Tr', 'Ct', 'Co', 'Di', 'Tf']
print(dataset.describe())
Ps Tr Ct Co Di Tf
count 732.000000 732.000000 732.000000 732.000000 7.320000e+02 732.000000
mean 7.418801 727.610416 8.056266 12.379825 7.563867e+10 22286.774041
std 7.705870 243.943093 1.111682 8.532508 5.491585e+10 23071.094095
min 0.150000 356.410000 5.883333 3.442916 1.681846e+10 1057.026608
25% 2.430000 499.281875 7.333333 7.574733 4.055572e+10 7382.009772
50% 4.914920 713.810010 7.875000 8.890402 4.969239e+10 12993.766448
75% 9.461703 864.820000 8.600000 13.035012 9.605659e+10 29144.912952
max 78.191470 1532.508000 14.130000 49.667654 2.094532e+11 136972.126998
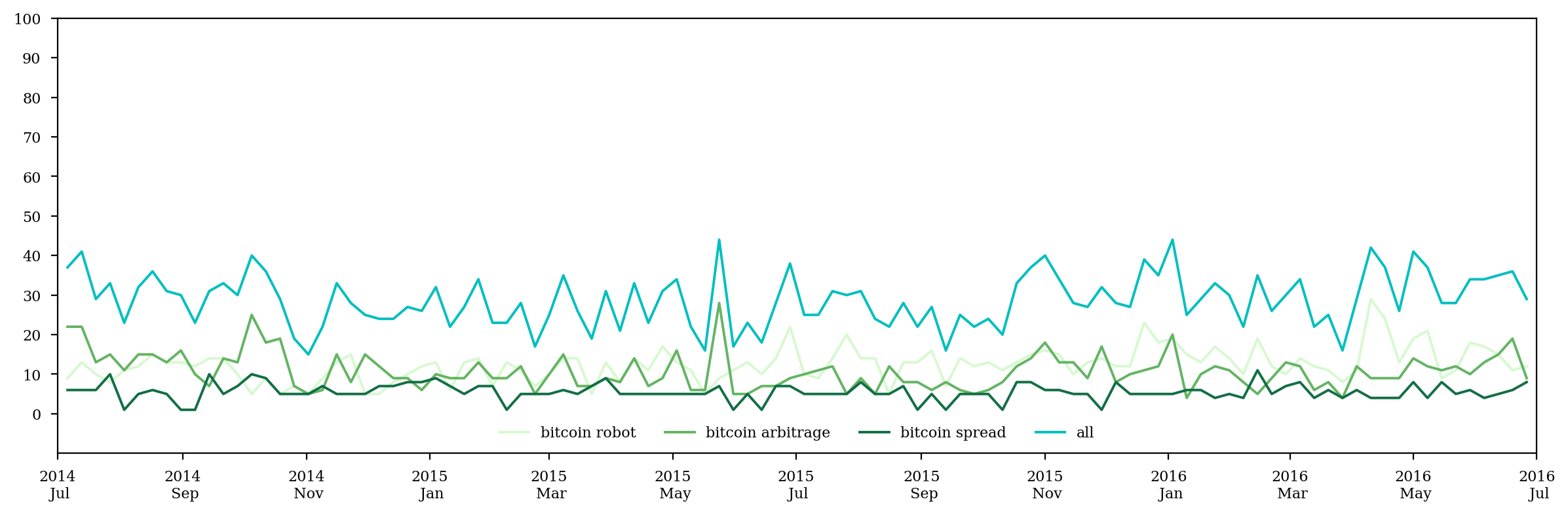
googletrends = []
kw_list = ['bitcoin robot', 'bitcoin arbitrage', 'bitcoin spread']
pytrend.build_payload(kw_list=kw_list)
googletrends = pytrend.interest_over_time().ix[start_date:end_date, :] + 1 # as googletrends can be 0 from time to time, which is troublesome for taking log
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(len(kw_list)):
ax.plot(googletrends.ix[:,i], c=cmocean.cm.algae(i/len(kw_list)), label=kw_list[i])
ax.plot(googletrends.sum(axis=1), c='c', label='all')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
plt.tight_layout()
plt.legend(loc='lower center', frameon=0, ncol=len(kw_list)+1)
plt.ylim(-10,100)
plt.yticks(range(0,101,10))
plt.savefig('multrend.pdf')
plt.show()
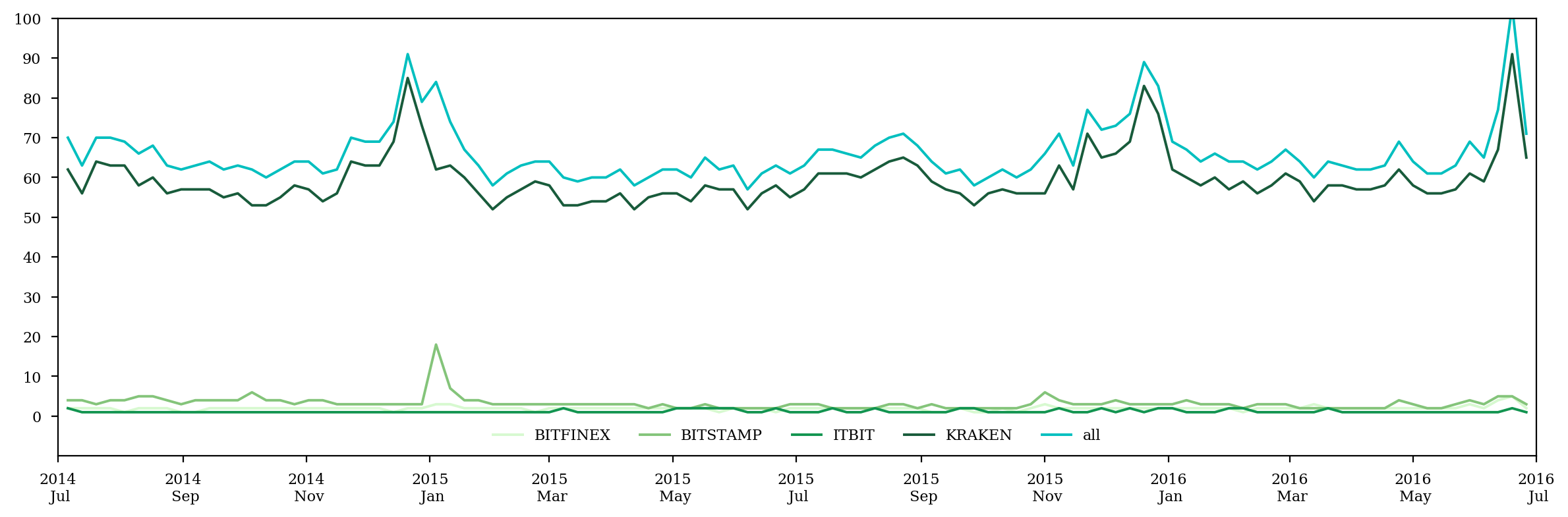
exchangetrends = []
kw_list = np.setdiff1d(exchangelist, ['ROCK'])
pytrend.build_payload(kw_list=kw_list)
exchangetrends = pytrend.interest_over_time().ix[start_date:end_date, :] + 1
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(len(kw_list)):
ax.plot(exchangetrends.ix[:,i], color=cmocean.cm.algae(i/len(kw_list)), label=kw_list[i])
ax.plot(exchangetrends.sum(axis=1), c='c', label='all')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
plt.tight_layout()
plt.legend(loc='lower center', frameon=0, ncol=len(kw_list)+1)
plt.ylim(-10,100)
plt.yticks(range(0,101,10))
plt.savefig('multrend.pdf')
plt.show()
dataset = pd.concat([dataset, googletrends.sum(axis=1), exchangetrends.sum(axis=1)], axis=1, join='outer').fillna(method='ffill').fillna(method='bfill')
dataset.columns = list(dataset.columns[:-2]) + ['Gt1', 'Gt2']
dataset.Gt1.interpolate(inplace=1)
dataset.Gt2.interpolate(inplace=1)
log_dataset = z_norm(np.log(dataset).rolling(5).mean().fillna(method='bfill'))
log_dataset.columns = ['Log'+c for c in log_dataset.columns]
print(log_dataset.describe())
LogPs LogTr LogCt LogCo LogDi LogTf LogGt1 LogGt2
count 7.320000e+02 7.320000e+02 7.320000e+02 7.320000e+02 7.320000e+02 7.320000e+02 7.320000e+02 7.320000e+02
mean -4.284976e-15 1.526951e-14 2.660744e-14 -2.311827e-16 5.078330e-14 -1.000566e-14 4.753939e-15 9.735989e-15
std 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
min -1.902323e+00 -1.600349e+00 -2.681378e+00 -1.602305e+00 -1.918163e+00 -2.449733e+00 -2.868102e+00 -1.541291e+00
25% -8.414662e-01 -1.003732e+00 -6.189083e-01 -6.491453e-01 -5.965383e-01 -7.432149e-01 -6.731405e-01 -6.369187e-01
50% -1.734537e-02 8.771289e-02 -2.819185e-02 -4.128926e-01 -2.796970e-01 -1.754303e-01 4.339693e-02 -2.954394e-01
75% 7.996859e-01 6.973955e-01 5.295034e-01 4.580167e-01 6.834602e-01 6.506610e-01 7.555832e-01 4.566839e-01
max 2.645812e+00 2.439251e+00 3.834172e+00 2.765270e+00 1.896075e+00 2.321454e+00 2.077746e+00 4.822614e+00
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure(figsize=(5,4))
ax = fig.add_subplot(111)
idx = log_dataset.corr().sort_values(by='LogPs', ascending=0).index
log_dataset = log_dataset.ix[:,idx]
corr = log_dataset.corr()
sns.heatmap(corr, square=1, ax=ax)
plt.yticks(rotation=0)
plt.xticks(rotation=90)
plt.tight_layout()
plt.savefig('mulcorr.pdf')
plt.show()
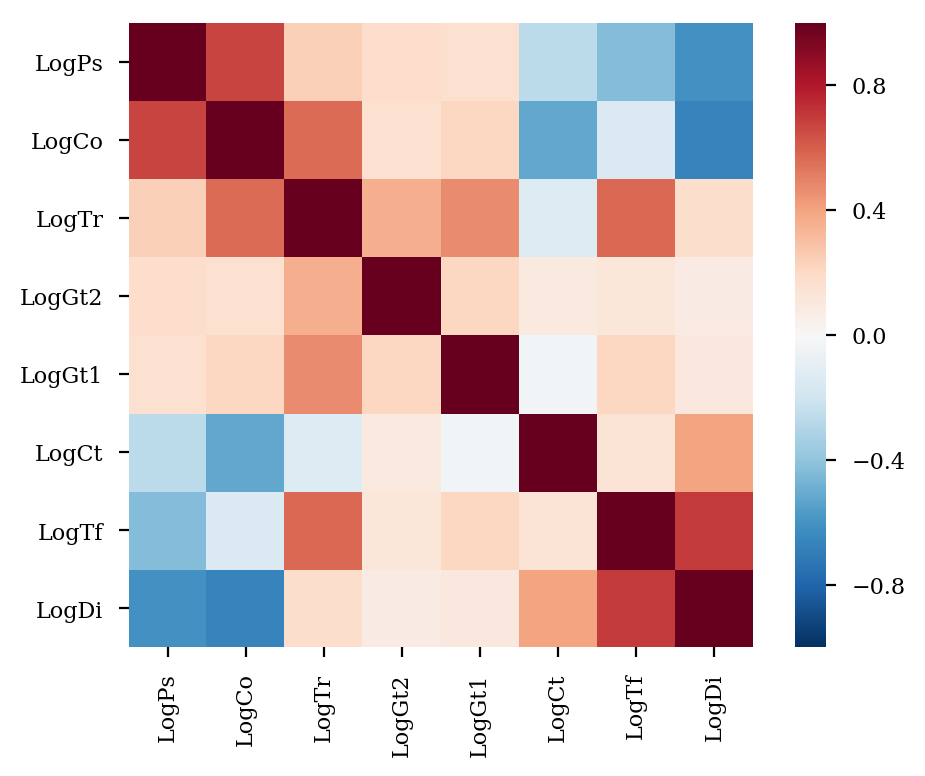
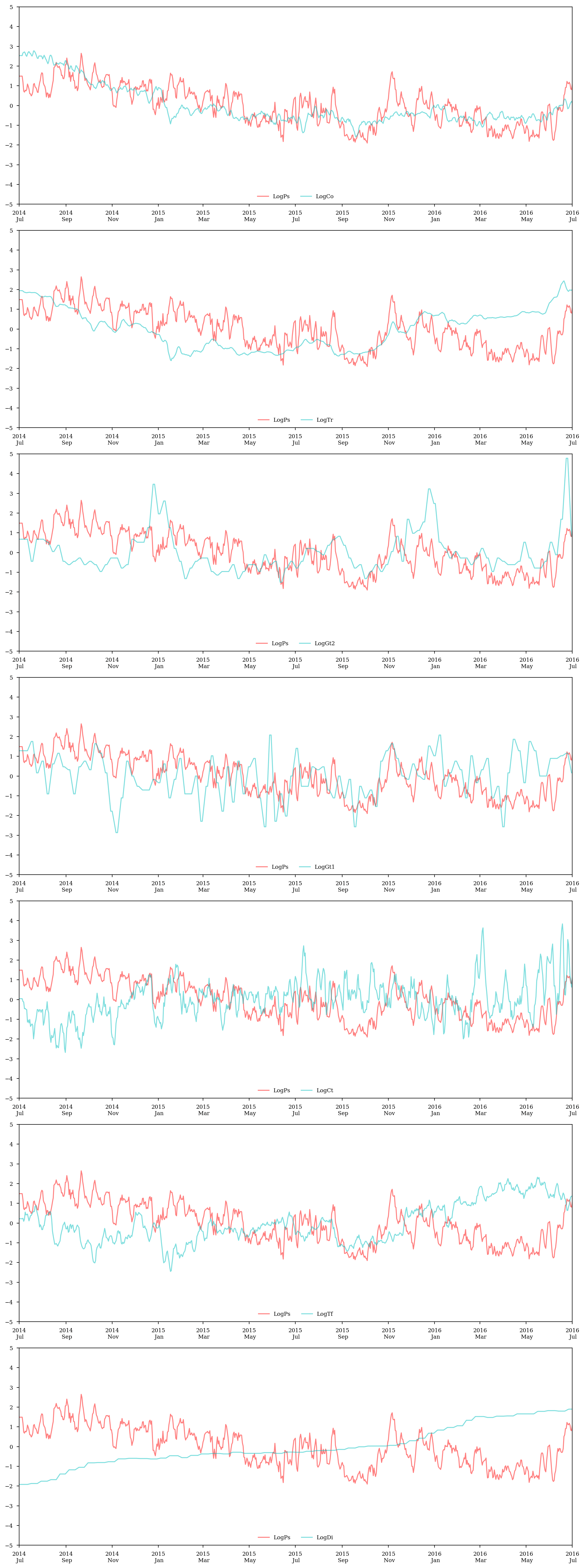
fig = plt.figure(figsize=(12,4*len(corr)))
for i in range(len(corr)-1):
ax = fig.add_subplot(len(corr)-1,1,i+1)
ax.plot(log_price_spread, c='r', label='LogPs', alpha=.5)
ax.plot(log_dataset.ix[:,i+1], c='c', alpha=.5, label=log_dataset.columns[i+1])
ax.legend(frameon=0,loc='lower center', ncol=2)
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
ax.set_ylim(-5,5)
ax.set_yticks(range(-5,6))
plt.tight_layout()
plt.show()
endog = log_dataset.LogPs
exog = log_dataset.ix[:,np.setdiff1d(log_dataset.columns,['LogPs'])]
train_endog = endog.ix[start_date:mid_date]
train_exog = exog.ix[start_date:mid_date]
test_endog = endog.ix[mid_date:end_date]
test_exog = exog.ix[mid_date:end_date]
min_aic = min_bic = 1e5
min_aic_order = min_bic_order = (0,0,0)
for p in range(1,10):
for q in range(3):
for d in range(1):
model = sm.tsa.SARIMAX(train_endog, train_exog, (p, d, q))
try:
result = model.fit(trend='nc')
result.summary()
except:
continue
stat = abs(sm.stats.durbin_watson(result.resid)-2)
stat_score = (stat <= 0.01) * 3 + (0.01 < stat <= 0.05) * 2 + (0.05 < stat <= 0.10) * 1
if np.abs(np.concatenate([result.arroots, result.maroots])).min() > 1.05:
aic = result.aic
bic = result.bic
if aic < min_aic:
min_aic = aic
min_aic_order = (p,d,q)
if bic < min_bic:
min_bic = bic
min_bic_order = (p,d,q)
print('({},{},{}) AIC = {:>7.2f}, BIC = {:>7.2f}, |DW-2| = {:.8f} {}'.format(p,d,q,aic,bic,stat,stat_score*'*'))
print()
print('Minimum AIC = {:.2f} at {}, minimum BIC = {:.2f} at {}'.format(min_aic, min_aic_order, min_bic, min_bic_order))
(1,0,0) AIC = 95.23, BIC = 134.02, |DW-2| = 0.32750528
(1,0,1) AIC = 82.47, BIC = 125.56, |DW-2| = 0.03040248 **
(1,0,2) AIC = 81.51, BIC = 128.92, |DW-2| = 0.01859667 **
(2,0,0) AIC = 79.67, BIC = 122.77, |DW-2| = 0.02601878 **
(2,0,1) AIC = 77.37, BIC = 124.78, |DW-2| = 0.02101876 **
(2,0,2) AIC = 77.46, BIC = 129.18, |DW-2| = 0.02477762 **
(3,0,0) AIC = 77.69, BIC = 125.10, |DW-2| = 0.00997169 ***
(3,0,1) AIC = 75.14, BIC = 126.85, |DW-2| = 0.00109986 ***
(4,0,0) AIC = 75.70, BIC = 127.42, |DW-2| = 0.00565012 ***
(4,0,1) AIC = 77.69, BIC = 133.72, |DW-2| = 0.00489150 ***
(5,0,0) AIC = 77.64, BIC = 133.67, |DW-2| = 0.00382267 ***
(5,0,1) AIC = 56.67, BIC = 117.01, |DW-2| = 0.11066651
(6,0,0) AIC = -11.64, BIC = 48.69, |DW-2| = 0.10243475
(6,0,1) AIC = -16.11, BIC = 48.54, |DW-2| = 0.02155382 **
(6,0,2) AIC = -16.40, BIC = 52.56, |DW-2| = 0.00558554 ***
(7,0,0) AIC = -18.40, BIC = 46.25, |DW-2| = 0.00766101 ***
(7,0,1) AIC = -16.75, BIC = 52.20, |DW-2| = 0.00203650 ***
(7,0,2) AIC = -15.06, BIC = 58.20, |DW-2| = 0.00505927 ***
(8,0,0) AIC = -17.85, BIC = 51.11, |DW-2| = 0.00599037 ***
(8,0,1) AIC = -21.57, BIC = 51.70, |DW-2| = 0.01490724 **
(8,0,2) AIC = -18.89, BIC = 58.69, |DW-2| = 0.02765866 **
(9,0,0) AIC = -15.87, BIC = 57.40, |DW-2| = 0.00530673 ***
(9,0,1) AIC = -20.02, BIC = 57.56, |DW-2| = 0.00183866 ***
(9,0,2) AIC = -17.87, BIC = 64.01, |DW-2| = 0.01105891 **
Minimum AIC = -21.57 at (8, 0, 1), minimum BIC = 46.25 at (7, 0, 0)
model = sm.tsa.SARIMAX(train_endog, train_exog, (8,0,1), freq='D')
result = model.fit(trend='nc')
print(result.summary())
Statespace Model Results
==============================================================================
Dep. Variable: LogPs No. Observations: 550
Model: SARIMAX(8, 0, 1) Log Likelihood 27.783
Date: Sun, 21 May 2017 AIC -21.566
Time: 01:13:14 BIC 51.703
Sample: 07-01-2014 HQIC 7.066
- 01-01-2016
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
LogCo 0.3659 0.181 2.024 0.043 0.012 0.720
LogCt 0.0089 0.039 0.224 0.823 -0.069 0.086
LogDi -0.0414 0.266 -0.156 0.876 -0.563 0.480
LogGt1 0.0069 0.061 0.113 0.910 -0.113 0.127
LogGt2 -0.0132 0.084 -0.157 0.875 -0.178 0.152
LogTf -0.3987 0.087 -4.557 0.000 -0.570 -0.227
LogTr 0.3262 0.180 1.815 0.069 -0.026 0.678
ar.L1 0.3475 0.168 2.063 0.039 0.017 0.678
ar.L2 0.7677 0.183 4.200 0.000 0.409 1.126
ar.L3 -0.1169 0.054 -2.171 0.030 -0.222 -0.011
ar.L4 -0.0721 0.051 -1.402 0.161 -0.173 0.029
ar.L5 -0.4598 0.047 -9.752 0.000 -0.552 -0.367
ar.L6 0.2162 0.088 2.468 0.014 0.045 0.388
ar.L7 0.3528 0.077 4.600 0.000 0.202 0.503
ar.L8 -0.1733 0.044 -3.953 0.000 -0.259 -0.087
ma.L1 0.7612 0.174 4.369 0.000 0.420 1.103
sigma2 0.0526 0.003 18.715 0.000 0.047 0.058
===================================================================================
Ljung-Box (Q): 138.21 Jarque-Bera (JB): 28.29
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 1.54 Skew: -0.30
Prob(H) (two-sided): 0.00 Kurtosis: 3.93
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
sm.stats.durbin_watson(result.resid)
1.9750927630586519
sm.stats.jarque_bera(result.resid)[1]
7.8859408081166919e-07
sm.stats.acorr_ljungbox(result.resid, lags=1)[1][0]
0.87455062641970893
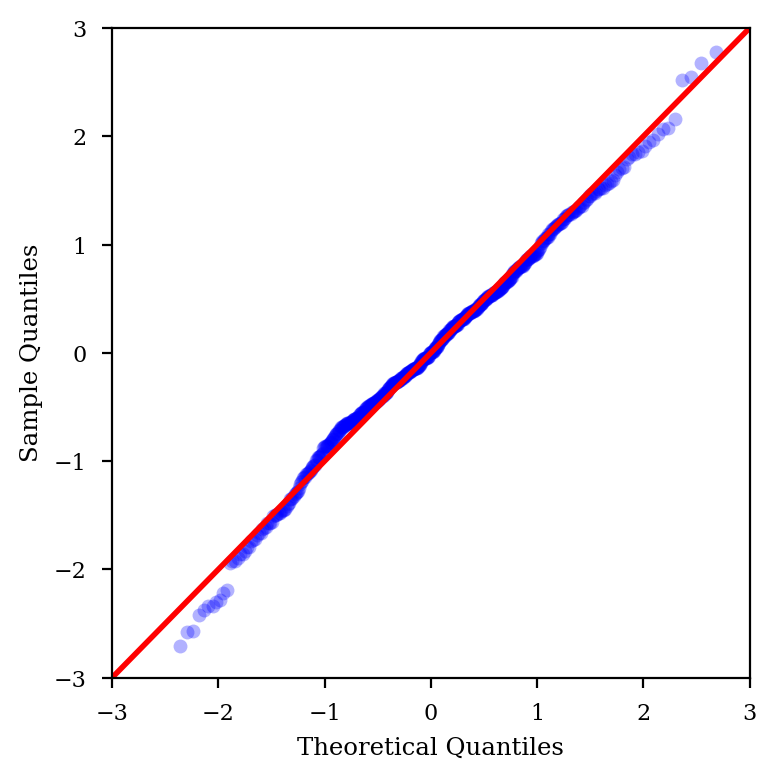
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(result.resid, line='45', ax=ax, fit=True)
lines = fig.findobj(lambda x: hasattr(x, 'get_color') and x.get_color() == 'r')
dots = fig.findobj(lambda x: hasattr(x, 'get_color') and x.get_color() == 'b')
[l.set_linewidth(2) for l in lines]
[d.set_alpha(0.3) for d in dots]
[d.set_markersize(5) for d in dots]
ax.set_ylim(-3,3)
ax.set_yticks(range(-3,4))
ax.set_xlim(-3,3)
ax.set_xticks(range(-3,4))
plt.tight_layout()
# plt.title('p-value = {}'.format(ss.normaltest(result.resid)[1]))
plt.savefig('mulqqplot.pdf')
plt.show()
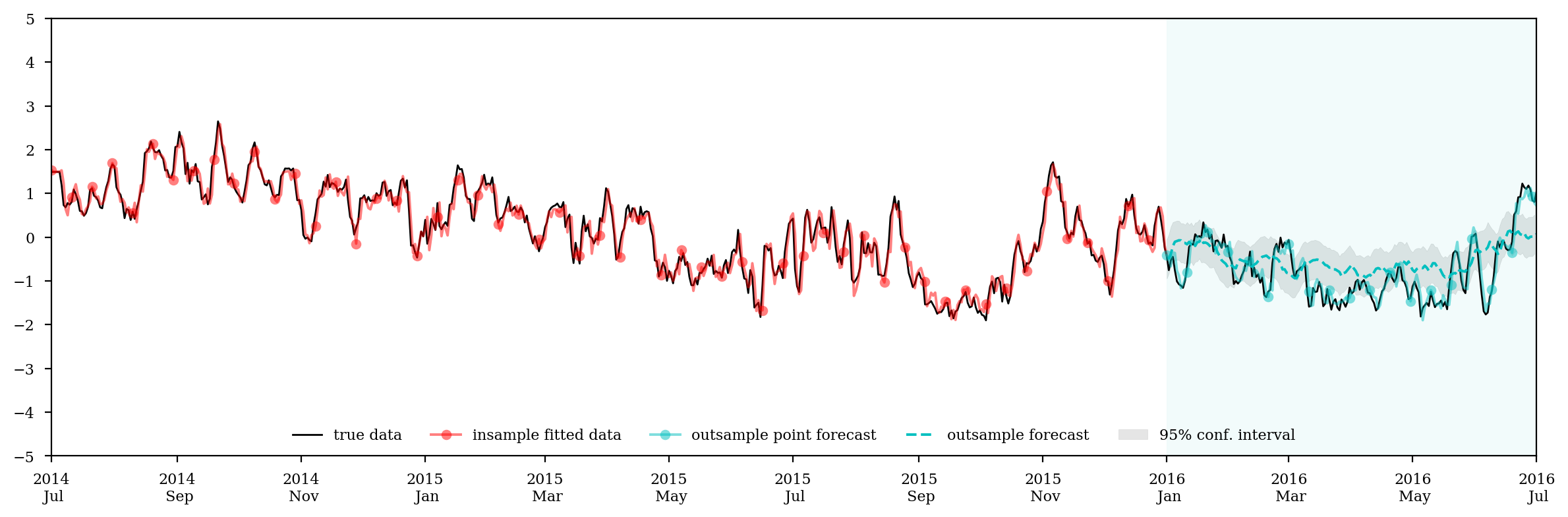
forecast = result.forecast(steps=len(test_endog), exog=test_exog)
fit = result.fittedvalues
model = sm.tsa.statespace.SARIMAX(endog, exog, model.order)
result = model.filter(result.params)
predict = result.get_prediction()
pred = predict.predicted_mean[mid_date:]
conf_interval = [forecast+predict.se_mean[len(train_endog):]*1.96,forecast-predict.se_mean[len(train_endog):]*1.96]
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(log_price_spread, c='k',lw=1, label='true data')
ax.plot(fit, 'ro-', markevery=10, alpha=0.5, label='insample fitted data')
ax.plot(pred, 'co-', markevery=10, alpha=0.5, label='outsample point forecast')
ax.plot(forecast, 'c--', label='outsample forecast')
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.fill_between(test_endog.index, conf_interval[0], conf_interval[1], color='k', alpha=.1, label='95% conf. interval')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(start_date, end_date)
ax.set_ylim(-5,5)
ax.set_yticks(range(-5,6))
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=5)
# plt.title('First Difference Log Price Spreads')
plt.savefig('mulfit1.pdf')
plt.show()
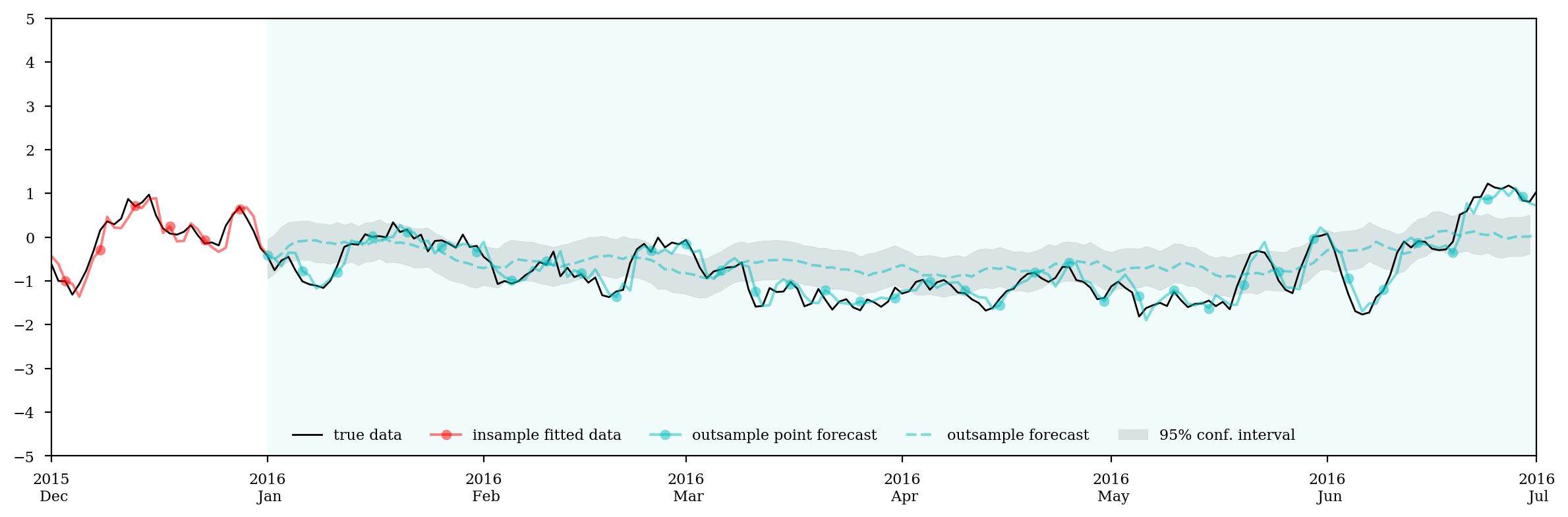
%config InlineBackend.figure_format = 'retina'
plt.close()
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(log_price_spread, c='k',lw=1, label='true data')
ax.plot(fit, 'ro-', markevery=5, alpha=0.5, label='insample fitted data')
ax.plot(pred, 'co-', markevery=5, alpha=0.5, label='outsample point forecast')
ax.plot(forecast, 'c--', alpha=0.5, label='outsample forecast')
ax.axvspan(mid_date, end_date, color='c', alpha=0.05)
ax.fill_between(test_endog.index, conf_interval[0], conf_interval[1], color='k', alpha=.1, label='95% conf. interval')
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=1))
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y\n %b'))
ax.set_xlim(temp_date, end_date)
ax.set_ylim(-5,5)
ax.set_yticks(range(-5,6))
plt.tight_layout()
plt.legend(loc='lower center', framealpha=0, ncol=5)
# plt.title('First Difference Log Price Spreads')
plt.savefig('mulfit2.pdf')
plt.show()
mase_mul_is = mase(train_endog, fit)
mase_mul_osp = mase(test_endog, pred)
mase_mul_os = mase(test_endog, forecast)
print('MASE insample is {:.3f}'.format(mase_mul_is))
print('MASE outsample is {:.3f}'.format(mase_mul_osp))
print('MASE outsample is {:.3f}'.format(mase_mul_os))
MASE insample is 0.858
MASE outsample is 0.857
MASE outsample is 2.688
uni = np.array([mase_uni_is, mase_uni_osp, mase_uni_os])
mul = np.array([mase_mul_is, mase_mul_osp, mase_mul_os])
print(uni)
print(mul)
[ 0.99605648 0.99134227 4.70378576]
[ 0.8576784 0.85705027 2.68798458]
plt.figure(figsize=(8,4))
plt.plot((0,0),(0,5),'#eeeeee',ls='--')
plt.plot((1,1),(0,5),'#eeeeee',ls='--')
plt.plot((2,2),(0,5),'#eeeeee',ls='--')
plt.plot(uni, 'ro-', label='univariate model')
plt.plot(mul, 'ko-', label='multivariate model')
plt.legend(loc='lower center', frameon=0, ncol=2)
plt.xticks(range(3),['insample', 'outsample point', 'outsample'])
# plt.title('MASE Scores')
plt.yticks(np.arange(0,6))
plt.ylim(0,5)
plt.tight_layout()
plt.savefig('mase.pdf')
plt.show()
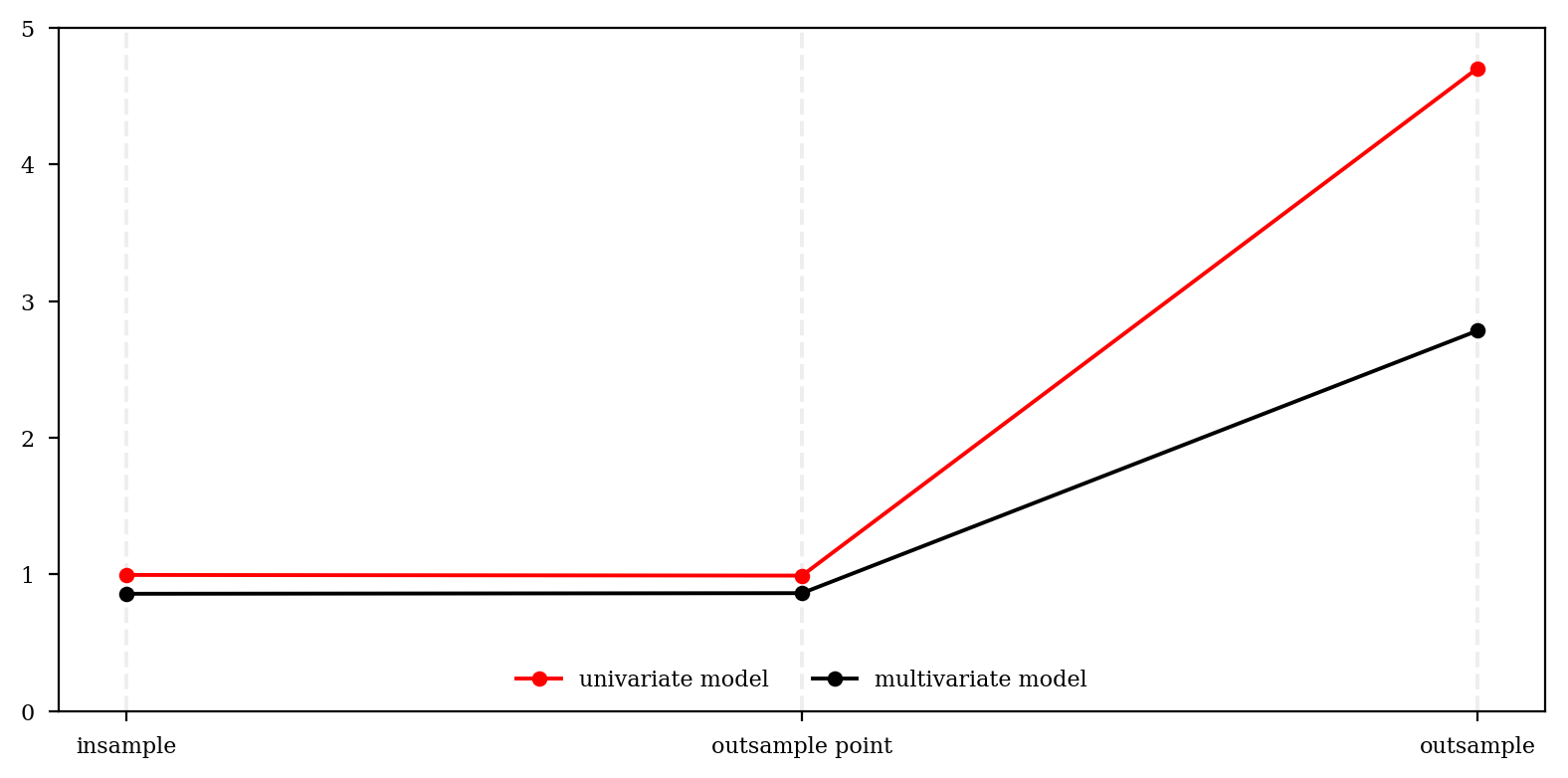
Step 6: Conclusion
So our exogenous indicators do work. We’ll see what else we can do with the multivariate model next time.
