Literature Review on Optimal Order Execution (2)
2018-04-29
Today, I’ll continue introducing papers about optimal order execution and particularly, in this post I’ll mainly walk through six papers by Rama Cont, respectively in 2010 and 2018. Professor Cont is renowned for his indepth research in stochastic analysis, stochastic processes and mathematical modeling in quantitative finance. He’s written dozens of papers concerning the order book dynamics by building rigorous mathematical models.
Rama Cont, Sasha Stoikov and Rishi Talreja (2010)
In this classic paper, the authors tried to model real-world order book as a discrete-time Markov chain. The order book is evenly divided into several buckets of prices, where order sizes are recalculated s.t. positive sizes represent ask orders, and negative sizes represent bid orders. Let’s denote this order book by $\mathbf{x}\in\mathbb{Z}^n$. Also, let $\mathbf{x}_{p\pm 1} \equiv \mathbf{x} \pm \mathbf{e}^p$ where $\mathbf{e}^p\in\mathbb{Z}^n$ is the $p$-th base vector. Denote the best ask and bid prices by $p^a$ and $p^b$. By assuming unit-sized orders1 and conditioning on the inflow of new orders, the Markov state transitioning can be described as below:
- A limit buy order at price
$p < p^a \Rightarrow \mathbf{x} \to \mathbf{x}_{p-1}$, - A limit sell order at price
$p > p^b \Rightarrow \mathbf{x} \to \mathbf{x}_{p+1}$, - A market buy order
$\Rightarrow \mathbf{x} \to \mathbf{x}_{p^a-1}$, - A market sell order
$\Rightarrow \mathbf{x} \to \mathbf{x}_{p^b+1}$, - A cancellation of an order at price
$p < p^a \Rightarrow \mathbf{x} \to \mathbf{x}_{p+1}$, - A cancellation of an order at price
$p > p^b \Rightarrow \mathbf{x} \to \mathbf{x}_{p-1}$.
Furthermore, the authors assumed stationary Poisson arrivals for these inflows in each bucket. Arrival rate for limit orders $\lambda(p)$ is an increasing function when $p$ is smaller than the current price, and is decreasing when $p$ is larger than the current price. Arrival rate for market orders is assumed to be constant $\mu$, and arrival rate for order cancellations should by assumption be proportional to the current order size in the underlying bucket of the book.
Therefore, we have
$\mathbf{x}\to \mathbf{x}_{p-1}$ at rate $\lambda(p^a-p)$for$p<p^a$,$\mathbf{x}\to \mathbf{x}_{p+1}$ at rate $\lambda(p-p^b)$for$p>p^b$,$\mathbf{x}\to \mathbf{x}_{p^a-1}$at rate$\mu$,$\mathbf{x}\to \mathbf{x}_{p^b+1}$at rate$\mu$,$\mathbf{x}\to \mathbf{x}_{p+1}$at rate$\theta(p^a - p)|x^p|$ for $p<p^a$,$\mathbf{x}\to \mathbf{x}_{p-1}$at rate$\theta(p-p^b)|x^p|$ for $p>p^b$.
The empirical performance of one-step ahead prediction is illustrated below.
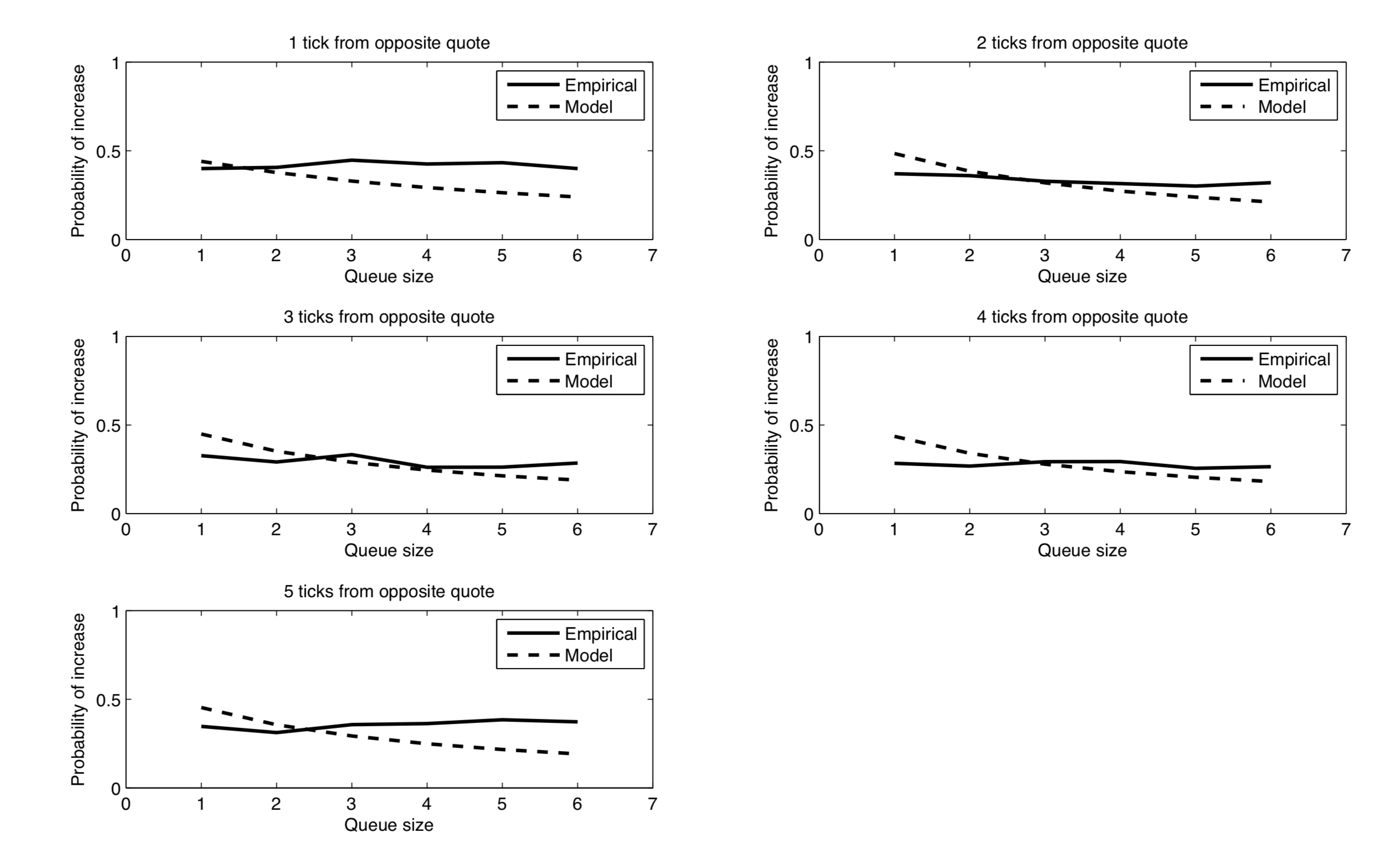
It is easy to recognize that the underlying random walk is a birth-death process. Hence, we may opt for Laplace transforms to calculate the first-passage times of our model, i.e. the time before our order is successfully executed given that the mid price hasn’t moved.
Rama Cont (2011)
In this paper of Cont, he tried to model untra-high frequency (UHF) order book using fluid and diffusion models.
| Regime | Time scale | Issues |
|---|---|---|
| Untra-high frequency | $\sim$ $10^{-3}$ to $1$ seconds |
Microstructure, latency |
| High frequency | $\sim$ $10$ to $10^2$ seconds |
Optimal execution |
| Daily | $\sim$ $10^3$ to $10^4$ seconds |
Trading strategies, option hedging |
By going from UHF to even more ideal data where we assume tick size $\to$ 0, order arrival frequency $\to\infty$ and order size $\to$ 0, we may apply multiple asymptotic theorems to analyze the order book dynamics in this very extreme case. Different combinations of scaling assumptions are possible for the same process and might lead to very different limits. Specifically, when we assume that variances vanishes asymptotically, the limit process is thus deterministic and often given by a PDE or ODE. This functional equivalent of Law of Large Numbers is called “fluid” or “hydrodynamic” limit, e.g.
$$ \lambda_n^i\sim n\lambda^i,\quad \left(\frac{N_1^n - N_2^n}{n}, t\ge 0\right) \overset{n\to\infty}{\to} ((\lambda^1 - \lambda^2)t, t\ge 0). $$
Other scaling assumption can lead to a totally different limit, e.g. “random” or “diffusion” limit:
$$ \lambda_n^i\sim n\lambda, \quad \lambda_n^1 - \lambda_n^2 = \sigma^2\sqrt{n},\quad \left(\frac{N_1^n - N_2^n}{\sqrt{n}}\right)\overset{n\to\infty}{\to}\sigma W. $$
Rama Cont and Adrien de Larrard (2013)
Similar to the first paper, here Cont and de Larrard tried to model order books as a Markov chain where limit orders, market orders and order cancellations arrives following stationary Poisson processes. Specifically, in this paper, the arrival rate of limit orders is constant. This is assumed in the hope of deriving close-form results analytically. Between each stock price change, we have $q_t^a$ and $q_t^b$ are independent birth-death processes with birth rate $\lambda$ and death rate $\mu+\theta$. Define $\sigma^a$ as the first-passage time for process $q_t^a$. Similarly define $\sigma^b$. Then, the time duration before the next price move is given by $\tau = \min\{\sigma^a, \sigma^b\}$.
Conditional Laplace transform of $\sigma^a$ solves
$$ \mathcal{L}(s, x) = \text{E}(\exp(-s\sigma^a)\mid q_0^a = x) = \frac{\lambda \mathcal{L}(s, x+1) + (\mu+\theta)\mathcal{L}(s,x-1)}{\lambda+\mu+\theta+s} $$
which eventually gives
$$ \mathcal{L}(s, x) = \left(\frac{(\lambda + \mu + \theta + s) - \sqrt{(\lambda + \mu + \theta + s)^2 - 4 \lambda (\mu + \theta)}}{2\lambda}\right)^x. $$
The distribution of $\tau$ conditional on the current queue length is
$$ \text{P}(\tau > t\mid q_0^a = x, q_0^b = y) = \text{P}(\sigma^a > t\mid q_0^a = x) \text{P}(\sigma^b > t\mid q_0^b = y) = \int_t^{\infty} \hat{\mathcal{L}}(u, x) du\int_t^{\infty} \hat{\mathcal{L}}(u, y) du $$
where the inverse Laplace transform $\hat{\mathcal{L}}$ is given by
$$ \hat{\mathcal{L}}(t, x) = \frac{x}{t} \sqrt{\left(\frac{\mu + \theta}{\lambda}\right)^x} I_x\left(2t\sqrt{\lambda(\theta + \mu)}\right)\exp(-t(\lambda + \mu + \theta)). $$
Rama Cont and Adrien de Larrard (2011 & 2012)
In the case of heavy-traffic queueing systems, the order books tend to show “diffusive” dynamics. In the most extreme scenario $\lambda = \mu + \theta$, we have
$$ \left(\frac{s_t(n\log n)}{\sqrt{n}}\right)_{t\ge 0} \overset{d}{\to} \sqrt{\frac{\pi \lambda \delta^2}{D(f)}B} $$
where $B$ is a Brownian motion, and
$$ D(f)\equiv \left(\int_{\mathbb{R}_+^2} xy\ dF(x, y)\right)^{1/2} $$
is the geometric mean of the bid and ask queue lengths. This directly gives a diffusion process with variance
$$ \sigma^2 = \delta^2 \frac{\pi\lambda}{D(f)}. $$
Interestingly, the formula does not require checking the stock price to estimate the volatility. Instead, all information it needs is from order flow statistics: arrival rate $\lambda$, and average order size $D(f)$.
Justin Sirignano and Rama Cont (2018)
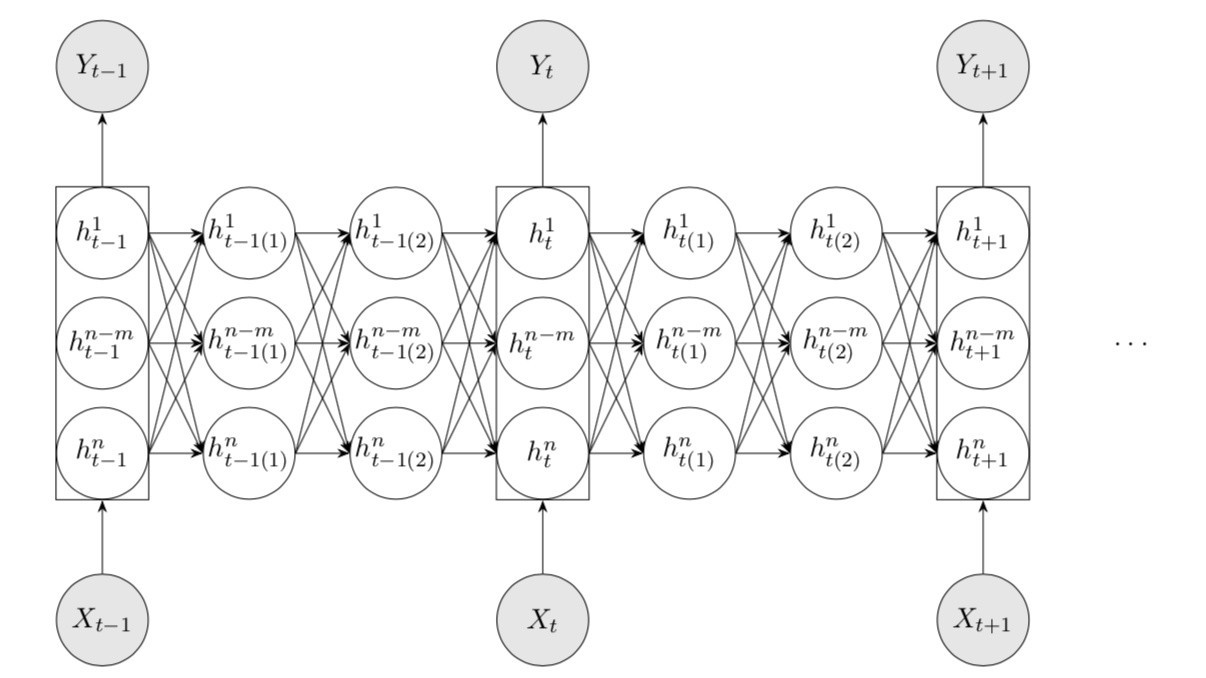
Deep learning is leading the fashion in academia. In the just-finished 6th Imperial-ETH Workshop in Mathematical Finance, Cont introduced his Long-Short-Term Memory (LSTM) network built with Sirignano that claimed to have defeated a range of other well-studied mathematical models (see below for the network structure). The model takes historical order book states as input and predicts next price moves. Specifically, they used the historical data from approximately 1,000 stocks traded on NASDAQ and trained the network asynchronously on over 500 GPUs. Results show significant improvement on prediction accuracy by introducing long-term memory into the model and moreover, a tendency of universal effectiveness even for stocks out of the sample.
References
- Rama Cont, Sasha Stoikov and Rishi Talreja. “A stochastic model for order book dynamics”. Operations Research, Volume 58, No. 3 (2010), 549-563.
- Rama Cont. “Statistical modeling of high frequency data: facts, models and challenges”. IEEE Sig. Proc., 28: 5 (2011), 16–25.
- Rama Cont, and Adrien de Larrard. “Price dynamics in a Markovian limit order market”. SIAM Journal on Financial Mathematics (2013), Vol 4, 1–25.
- Rama Cont, and Adrien De Larrard. “Order book dynamics in liquid markets: limit theorems and diffusion approximations” (2011).
- Rama Cont, and Adrien de Larrard. “Price dynamics in limit order markets: linking volatility with order flow”. Working Paper (2012).
- Justin Sirignano, and Rama Cont. “Universal features of price formation in financial markets: perspectives from Deep Learning” (2018).
-
It is apparently a very strong assumption. Although according to the paper, the authors used average order size as the unit in empirical validation of the model, I still doubt whether assuming universally constant order size shall be a good idea. ↩︎
